第 3 章 鸽巢原理

EX1

Concerning Application 4, show that there is a succession of days during which the chess master will have played exactly k games, for each k = 1,2, ... ,21. (The case k = 21 is the case treated in Application 4.) Is it possible to conclude that there is a succession of days during which the chess master will have played exactly 22 games?

参考答案给出的思路，记$b_i$表示第 i 天所下盘数且$b_i\ge 1$，可以考虑两组单增序列，

$$\begin{array}{}\text{(1)}& \{b_1+b_2+\cdots +b_i\},1\le i\le 77\end{array}$$

和

$$\begin{array}{}\text{(2)}& \{b_0+b_2+\cdots +b_j+k\},0\le j\le 76,b_0=0\end{array}$$

每组序列都满足单增且大小都为 77，序列 (1) 中没有重复元素，序列 (2) 中也没有重复元素。

序列 (1) 的上界为$12\times 11=132$， 序列 (2) 的上界 S 满足$S<b_1+b_2+\cdots +b_{77}+k\le 12\times 11+22=154$， 同时 S 为整数，可以得到$S\le 153$。

综上，序列 (1) 和序列 (2) 的上界为 153，也即最多有 153 个不同的数。而序列中一共有 154 个数， 由鸽巢原理序列 (1) 中至少有一个数$b_1+b_2+\cdots +b_y$ 与序列 (2) 中的某个数$b_1+b_2+\cdots +b_x+k$相同，满足，

$$b_1+b_2+\cdots +b_y=b_1+b_2+\cdots +b_x+k$$

可以求出，

$$k=b_{x+1}+\cdots +b_y$$

一个不太完善的想法 💊

我们采用和书上一致的证法，设$a_i$是从第一天开始到第 i 天下棋总数，因此有，

$$\begin{array}{}\text{(1)}& 1\le a_1<a_2<\cdots <a_{77}\le 12\times 11=132\end{array}$$

之后考虑序列

$$\begin{array}{}\text{(2)}& 1\le k<a_1+k<a_2+k<\cdots <a_{77}+k\le 132+k\end{array}$$

序列 (1) 和序列 (2) 中的所有元素一定落在区间[1, 132+k]，且序列中一共有$77\times 2=154$个元素，因此只要 154 > 132 + k 就满足鸽巢原理，此时，k < 21。

这个时候会漏掉 k=22 的情况，解决方案就是像参考答案一样，考虑压缩序列 (2) 的范围我们只选择从$a_1$到$a_{76}$的部分。那么有，

$$\begin{array}{}\text{(3)}& 1\le k<a_1+k<a_2+k<\cdots <a_{76}+k<a_{77}+k\le 132+k\le 154\end{array}$$

这时候选择的部分不是$a_1+k$到$a_{77}+k$， 而是$k$到$a_{76}+k$，仍然是 77 个元素。 结合序列 (1) 和序列 (3)，就能找出存在$a_x=a_y+k$。 当然，要补充定义$a_0=0$。

EX2 ⭐

* Concerning Application 5, show that if 100 integers are chosen from 1,2, ... ,200, and one of the integers chosen is less than 16, then there are two chosen numbers such that one of them is divisible by the other.

EX3

Generalize Application 5 by choosing (how many?) integers from the set {1, 2, ..., 2n}.

至少选择 n+1 个数来保证它们中的一个能被另一个整除。

因为任意一个整数都可以写成$2^k\cdot a$的形式，因此可以根据指数 k 进行划分集合，同一集合里的数一定存在一个数能被另一个数整除。

$$S_a=\{2^k\cdot a|k\ge 0,a\text{ is odd}\}$$

对于从 1 到 2n 的整数，a 的取值为 1，3，5，...，2n-1，共有 n 个集合，由鸽巢原理，n+1 个数至少存在 2 个数落在同一集合中。

EX4

Show that if n + 1 integers are chosen from the set {1, 2, ... , 2n}, then there are always two which differ by 1.

记从集合中选取的数为$a_i$，并且假设$a_{i+1}-a_i\ge 2$，此外有，

$$1\le a_1<a_2<\cdots <a_n<a_{n+1}\le 2n$$

可以得出范围$a_{n+1}-a_1\le 2n-1$，然而，

$$(a_{n+1}-a_n)+(a_n-a_{n-1})+\cdots +(a_2-a_1)=a_{n+1}-a_1\ge 2n$$

与上述中的范围矛盾，因此假设不成立。

采用鸽巢原理进行集合划分，把集合划分成$S_i=\{2i-1,2i\},1\le i\le n$， 显然集合均不相交，且一共有 n 个集合，那么 n+1 个数一定满足至少有两个数落在同一集合。

EX5

Show that if n + 1 distinct integers are chosen from the set {1, 2, ... , 3n}, then there are always two which differ by at most 2.

同上，可以把集合进行划分，并使用鸽巢原理。

$$S_i=\{3i-2,3i-1,3i\},1\le i\le n$$

EX6

Generalize Exercises 4 and 5.

Show that if n + 1 integers are chosen from the set {1, 2, ... , kn}, then there are always two which differ by at most k-1(in other words, kess than k).

把集合按照如下方式进行划分，再使用鸽巢原理。

$$S_i=\{ki-(k-1),\cdots ,ki-1,ki\},1\le i\le n$$

EX7 ⭐

* Show that for any given 52 integers there exist two of them whose sum, or else whose difference, is divisible by 100.

EX8

Use the pigeonhole principle to prove that the decimal expansion of a rational number min eventually is repeating. For example,

$$\frac{34,478}{99,900}=0.34512512512512512·...$$

将分数记为两个正整数 m 和 n 的比值，即 m/n。 对于整数$i=0,1,\cdots ,n$，考察分数${10}^{i}m/n$，并且记余数为$r_i$。 显然余数的取值范围是$r_i=0,1,\cdots ,n-1$，一共有 n 个， 因此由鸽巢原理可以断定，存在整数 $i,j(0\le i<j\le n)$ 满足 $r_i=r_j$。

之后考虑分数$({10}^{j}m-{10}^{i}m)/n$，并且记$s=j-i$， 这样存在整数 q 满足${10}^i({10}^s-1)m=nq$，并且记$q/({10}^s-1)$的余数为 r。 同样可以判断 r 的取值范围是$r=0,1,\cdots ,{10}^s-2$。可以写作$q=b({10}^s-1)+r$。

那么分数${10}^{i}m/n$就可以展开为等比级数的和，

$$\begin{array}{rl}\frac{{10}^{i}m}{n}=& \frac{q}{{10}^s-1}\\ =& b+\frac{r}{{10}^s-1}\\ =& b+\frac{r}{{10}^s}+\frac{r}{{10}^{2s}}+\frac{r}{{10}^{3s}}+\cdots \frac{r}{{10}^{ns}}+\cdots \end{array}$$

所以，${10}^{i}m/n$可以表示为循环小数的形式，循环部分的长度是 j-i，那么 m/n 是${10}^{i}m/n$小数点左移 i 位，不改变循环部分，因此最终也是循环的。

提示

p44 鸽巢原理的推论证明。

EX9

In a room there are 10 people, none of whom are older than 60 (ages are given in whole numbers only) but each of whom is at least 1 year old.Prove that we can always find two groups of people (with no common person) the sum of whose ages is the same.Can 10 be replaced by a smaller number?

考虑 10 个人划分组的所有情况，一共有$2^{10}=1024$种组， 对于所有的组年龄总和一定在 0 和 600 之间，那么由鸽巢原理，一定能找到两种组的划分使组中的年龄之和相等。

EX10

A child watches TV at least one hour each day for seven weeks but, because of parental rules, never more than 11 hours in anyone week. Prove that there is some period of consecutive days in which the child watches exactly 20 hours of TV. (It is assumed that the child watches TV for a whole number of hours each day.)

本质还是大师下棋问题，我们设$a_i$是从第一天到第 i 天一共看电视$a_i$小时，那么有

$$1\le a_1<a_2\cdots <a_{77}\le 7\times 11=77$$

同时，考虑如下序列，

$$21\le a_1+20<a_2+20<\cdots <a_{77}+20\le 97$$

两组序列一共有 154 个数，每个序列严格递增，并且都在区间[1, 97]中， 由鸽巢原理一定存在 i 和 j 满足 $a_j=a_i+20$，也即从第 i+1 天到第 j 天恰好看 20 个小时电视。

EX10PS

本题条件比 EX1「宽松」很多。

EX11

A student has 37 days to prepare for an examination. From past experience she knows that she will require no more than 60 hours of study. She also wishes to study at least 1 hour per day. Show that no matter how she schedules her study time (a whole number of hours per d!1y, however), there is a succession of days during which she will have studied exactly 13 hours.

仍旧是大师下棋问题，这次我们练习另一种解法。

记$b_i$表示第 i 天学习的时间且$b_i\ge 1$，可以考虑两组单增序列，

$$\begin{array}{}\text{(1)}& \{b_1+b_2+\cdots +b_i\},1\le i\le 37\end{array}$$

和

$$\begin{array}{}\text{(2)}& \{b_0+b_2+\cdots +b_j+13\},0\le j\le 36\end{array}$$

显然两组序列单增，并且范围在[1, 73]之间，并且一共有 74 个序列，那么一定存在分别来自 (1) 和 (2) 的两个序列，使得

$$b_1+b_2+\cdots +b_i=b_0+b_2+\cdots +b_j+13$$

也即从第 j+1 天到第 i 天一共学习 13 小时。

EX12

Show by example that the conclusion of the Chinese remainder theorem (Application 6) need not hold when m and n are not relatively prime.

采用反证法证明该结论不成立，举例取 m=4, n = 6， 因此$a\in \{0,1,2,3\},b\in \{0,1,2,3,4,5\}$，我们分别从集合中去取 a 和 b，使 a+b 为奇数。 并且假设存在这样的 x 同时满足 x = 4p + a 和 x = 6q + b， 两式相加并整理可以得到 2x - 4p - 6q = a + b，等式左边为偶数，右边为奇数显然不合理，因此假设不成立。

EX13 ⭐

* Let S be a set of six points in the plane, with no three of the points collinear. Color either red or blue each of the 15 line segments determined by the points of S. Show that there are at least two triangles determined by points of S which are either red triangles or blue triangles. (Both may be red, or both may be blue, or one may be red and the other blue.)

EX14

A bag contains 100 apples, 100 bananas, 100 oranges, and 100 pears. If I pick one piece of fruit out of the bag every minute, how long will it be before I am assured of having picked at least a dozen pieces of fruit of the same kind?

由极端原理，考虑最差的情况所有水果都只取出了 11 个，此时花费 44 分钟。 那么下一次一定会出现一打相同种类的水果，即至少 45 分钟会拿出一打相同水果。

EX15

Prove that, for any n + 1 integers $a_1,a_2,\cdots ,a_{n+1}$, there exist two of the integers $a_i$ and $a_j$ with $i\ne j$ such that $a_i-a_j$ is divisible by n.

对于任意整数，总可以写成$a_i=p_{i}n+r_i$，其中$0\le r_i\le n-1$且$r_i$为整数。 由鸽巢原理，n+1 个数模 n 的余数中一定能找到两个数余数相同，此时有

$$a_j-a_i=(p_{j}n+r_j)-(p_{i}n+r_i)=(p_j-p_i)n$$

即两数之差被 n 整除。

EX16

Prove that in a group of n > 1 people there are two who have the same number of acquaintances in the group. (It is assumed that no one is acquainted with oneself. )

一共有 n 个人，那么可能认识人数的集合为$\{0,1,\cdots ,n-1\}$。

假设每个人认识的人数都不同，那么我们会发现存在 Alice 并不认识任何人而 Bob 认识所有人的矛盾情况，因此假设不成立。

EX16PS

需要强调的是题目中的认识关系是相互的，也就是说我认识你就等于你认识我，不存在我认识你而你不认识我的情况。

EX17

There are 100 people at a party. Each person has an even number (possibly zero) of acquaintances. Prove that there are three people at the party with the same number of acquaintances.

考虑按照认识的人数划分集合，记$f(idx)=2k$表示第 idx 人认识的人数是 2k，一共有 50 个集合。

$$S_{2k}=\{idx|f(idx)=2k\}，0\le k\le 49$$

显然如果某个集合$|S_{2i}|\ge 3$，满足题意。下面考察所有集合$|S_{2k}|<3$的情况。

如果存在$|S_i|\le 1$，那么剩余 99 人（或 100 人）一定落在其他集合中，由鸽巢原理增强版知$\lceil {\displaystyle \frac{99}{49}}\rceil =3$，一定存在某个集合满足$|S_j|\ge 3$，与假设矛盾。

那么，所有集合的大小只能为 2，则出现$|S_0|=|S_{98}|=2$，即会出现聚会中的两人不认识任何人，这限制了其他人最多认识 96 个人，即$|S_{98}|=0$与所有集合大小为 2 条件矛盾，因此不存在所有集合$|S_{2k}|\le 2$的情况。

EX18

Prove that of any five points chosen within a square of side length 2, there are two whose distance apart is at most $\sqrt{2}$.

把 2×2 的正方形划分为 4 个 1×1 的正方形，由鸽巢原理，存在一个正方形内至少有两个点，而同一个小正方形中最远的距离是$\sqrt{2}$。

EX19

(a) Prove that of any five points chosen within an equilateral(等边的) triangle of side length 1, there are two whose distance apart is at most ${\displaystyle \frac{1}{2}}$.

(b) Prove that of any 10 points chosen within an equilateral triangle of side length 1, there are two whose distance apart is at most ${\displaystyle \frac{1}{3}}$.

(c) Determine an integer mn such that if mn points are chosen within an equilateral triangle of side length 1, there are two whose distance apart is at most 1/n.

EX19Q(a)&Q(b)

根据 EX18 的做法，题目的关键是如何分割等边三角形，分割方法如下。

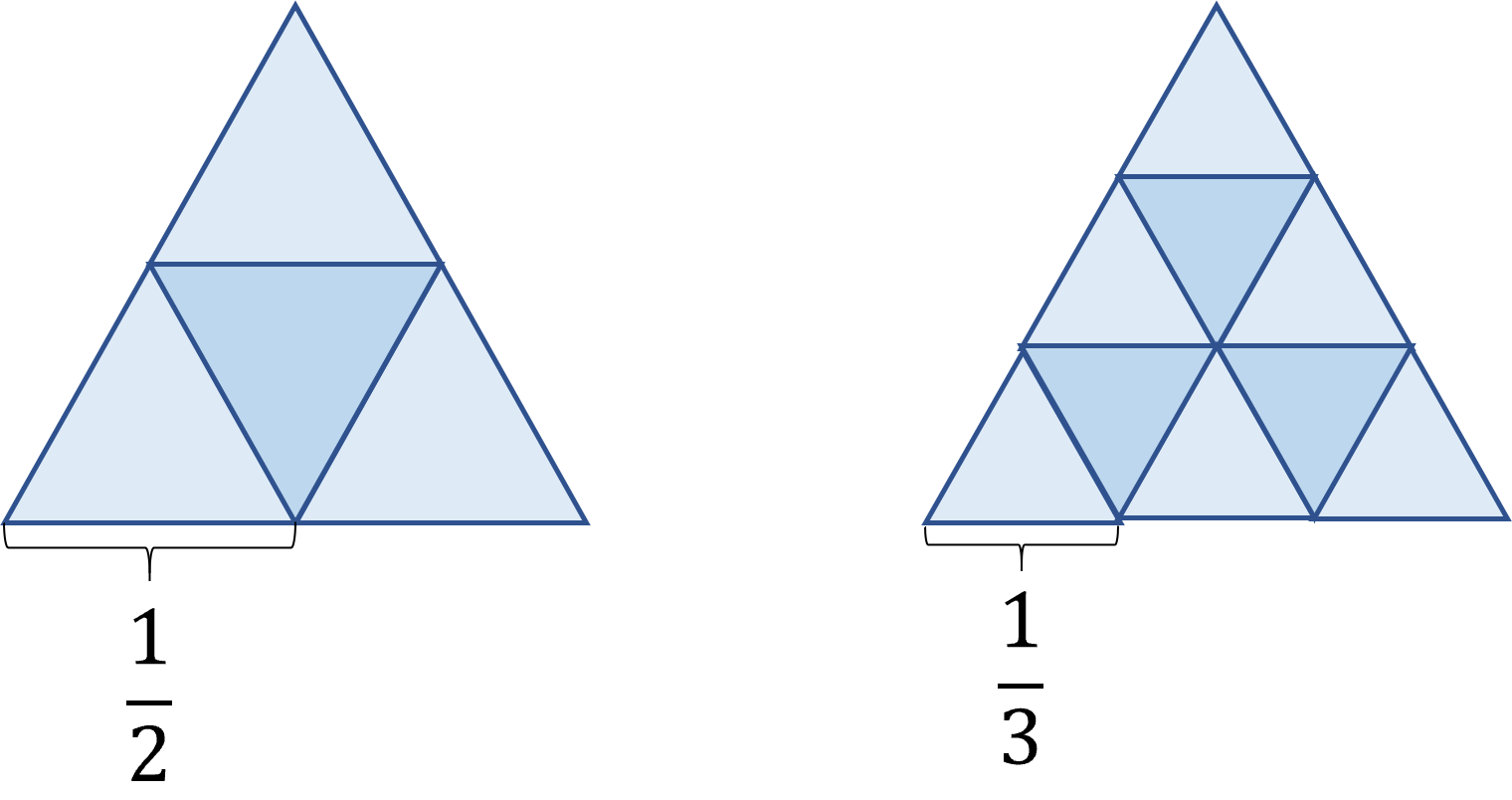
EX19Q(c)

只需要把每条边 n 等分，然后平行于另外两条边做平行线。 考虑到等边三角形的面积公式为${\displaystyle \frac{\sqrt{3}}{4}}{a}^2$，其中 a 为边长，分割前后总面积相同。

$${\displaystyle \frac{\sqrt{3}}{4}}{1}^2={\displaystyle \frac{\sqrt{3}}{4}}{(\frac{1}{n})}^{2}x$$

一共分割出$n^2$个小等边三角形，因此可以取$m_n=n^2+1$，使之符合鸽巢 原理。

EX20

Prove that $r(3,3,3)\le 17$.

考虑$K_{17}\to K_3,K_3,K_3$，并且使用红色、蓝色和绿色进行染色。

任选一个点 x，与它相连的边有 16 条，由鸽巢原理加强版可知，至少存在$\lceil {\displaystyle \frac{16}{3}}\rceil =6$条边的颜色相同，不妨设为红色。

那么对于与 x 相连的点$\{x_i{\}}_{i=1}^6$，如果他们之中的连线存在一条红边，则该条边上的两点和 x 则可以构成一个$K_3$；否则（即不存在红边），由$r(3,3)=6$可知，6 个顶点染色一定可以构造出一个蓝色或绿色的$K_3$。

综上，17 个点可以构造出$K_3$，不少于 17 个点也一定能构造出$K_3$，即$r(3,3,3)\le 17$。

EX20PS

首先要知道各个符号的含义，$K_{17}\to K_3,K_3,K_3$中有 3 个$K_3$，它们是「或者」的关系，只需要证明一定存在某个$K_3$就好，而不是全部颜色同时构造出$K_3$。

第二点就是证明的是小于等于而不是等于，后者还需要证明 16 个点不一定存在$K_3$，参考 p49 正文部分。

EX21 ⭐

* Prove that r(3, 3, 3) 2: 17 by exhibiting a coloring, with colors red, blue, and green, of the line segments joining 16 points with the property that there do not exist three points such that the three line segments joining them are all colored the same.

EX22

Prove that

$$r\underset{\text{k+1}}{\underbrace{(3,3,\cdots ,3)}}\le (k+1)(r\underset{\text{k}}{\underbrace{(3,3,\cdots ,3)}}-1)+2$$

Use this result to obtain an upper bound for

$$r\underset{\text{n}}{\underbrace{(3,3,\cdots ,3)}}$$

仿照答案进行回答，记

$$n=r_k=r\underset{\text{k}}{\underbrace{(3,3,\cdots ,3)}},m=(k+1)(n-1)+2$$

考虑仿造 EX20 构造，

$$K_m\to \underset{\text{k+1}}{\underbrace{K_3,K_3,\cdots ,K_3}}$$

任取一点 x，与它相连的 m-1 条边中至少有 n 条具有相同颜色 （鸽巢原理加强版$\lceil {\displaystyle \frac{m-1}{k+1}}\rceil =\lceil {\displaystyle \frac{(k+1)(n-1)+1}{k+1}}\rceil =\lceil n-1+{\displaystyle \frac{1}{k+1}}\rceil =n$）， 记该颜色为$C_1$。 那么对于与 x 相连的点$\{x_i{\}}_{i=1}^n$，如果他们之中的连线存在一条$C_1$色边， 则该条边上的两点和 x 则可以构成一个$K_3$； 否则（即不存在$C_1$色边），由$r_k=n$可知，n 个顶点染色一定可以构造出一个$C_i$色$(2\le i\le k+1)$的$K_3$。

因此有$r_{k+1}\le m$，即，

$$r_{k+1}=r\underset{\text{k+1}}{\underbrace{(3,3,\cdots ,3)}}\le m=(k+1)(n-1)+2=(k+1)(r\underset{\text{k}}{\underbrace{(3,3,\cdots ,3)}}-1)+2$$

下面求$r_n$的上界（下面的 n 与上面的 n 无关，更接近上面的 k，上面使用 m 和 n 是为了和参考答案保持一致）。

目前由上面的证明已知$r_n\le n(r_{n-1}-1)+2$，还有一个边界条件$r_2=r(3,3)=6$。

$$\{\begin{array}{l}{r}_n-2\le n(r_{n-1}-1)\\ n(r_{n-1}-2)\le n(n-1)(r_{n-2}-1)\\ n(n-1)(r_{n-2}-2)\le n(n-1)(n-2)(r_{n-3}-1)\\ \cdots \\ n(n-1)\times \cdots \times 4(r_3-2)\le n(n-1)\times \cdots \times 3(r_2-1)\end{array}$$

不等式两边分别求和得，

$$r_n-2-n-n(n-1)-n(n-1)(n-2)-\cdots -n(n-1)\times \cdots \times 4\le n(n-1)\times \cdots \times 3\times 5$$

移项整理，并用排列数表示，

$$\begin{array}{rl}{r}_n\le & 2+n+n(n-1)+n(n-1)(n-2)+\cdots +n(n-1)\times \cdots \times 4+(n-1)\times \cdots \times 3\times 5\\ =& 2+\frac{n!}{(n-1)!}+\frac{n!}{(n-2)!}+\cdots \frac{n!}{3!}+5\times \frac{n!}{2!}\\ =& \frac{5}{2}n!+\sum _{i=1}^{n-3}\frac{n!}{n-i}+2\end{array}$$

EX23

The line segments joining 10 points are arbitrarily colored red or blue. Prove that there must exist three points such that the three line segments joining them are all red, or four points such that the six line segments joining them are all blue (that is, $r(3,4)\le 10$).

带入公式，显然有上述结论。

$$r(m,n)\le (\genfrac{}{}{0ex}{}{m+n-2}{n-1})=(\genfrac{}{}{0ex}{}{m+n-2}{n-1})$$

但是证明这个不等式本身也很复杂（试卷上写不开），所以还是考虑使用定义证明。

还是任取一点 x，记与 x 相连的 9 条线中红色的线有 m 条，蓝色的线有 n 条，并且 m+n=9 进行分类讨论。

当$m\ge 4$时，$n=9-m\le 5$，如果 m 条红边相连的点组成的$K_m$中存在一条红边，则可以选择该红边上的两点与 x 组成红色的$K_3$；否则（不存在红边），则$K_m$全为蓝边，则容易找出一个蓝色的$K_4$。

当$m\le 3$时，$n=9-m\ge 6$，n 条蓝边相连的点组成$K_n$，由$K_6\to K_3,K_3$可知，$K_n$中要么存在一个红色$K_3$（符合题意）；要么存在一个蓝色$K_3$，则该蓝色$K_3$与 x 又构成了蓝色$K_4$。

综上，$r(3,4)\le 10$。

EX23PS

Q：为什么想到根据$m\ge 4$进行分类讨论？

A：我想说，要是不看前人的解答，我也想不出来。 因为直观想法也是根据鸽巢原理加强版计算出可能的边界是$\lceil {\displaystyle \frac{9}{2}}\rceil =5$，之后进行讨论。 或许是考虑到红色的较少（红色的$K_3$，而不是蓝色的$K_3$），讨论了红色较少的分类。

EX24

Let $q_3$ and t be positive integers with $q_3\ge t$. Determine the Ramsey number $r_t(t,t,q_3)$.

先说结论$r_t(t,t,q_3)=q_3$，采用红色、蓝色和绿色染色，之后分别求下界和上界。

考虑全都使用绿色给$K_{q_3-1}$染色， 此时不存在红色$K_t^t$，不存在蓝色$K_t^t$， 也不存在绿色$K_{q_3}^t$， 因此$r_t(t,t,q_3)\ge q_3$。

考虑$K_{q_3}$中所有的大小为 t 的子集， 使用红色、蓝色和绿色进行染色，如果存在红色或蓝色$K_t^t$（只需要找到 t 个元素，全都为红色或蓝色即可）， 则满足$r_t(t,t,q_3)\le t\le q_3$； 否则所有 t 个元素的子集均为绿色， 即存在绿色$K_{q_3}^t$（存在$q_3$个元素，它所有 t 元素子集为绿色）， 也有$r_t(t,t,q_3)\le q_3$。

综上，有$r_t(t,t,q_3)=q_3$。

EX24PS

参考链接中的回答，突然意识到$r_t(\cdots )$与$r(\cdots )$是不同的，前者的概念参考 p50 页正文，t 子集。

EX25

Let $q_1,q_2,\cdots ,q_k,t$ be positive integers, where $q_1\ge t,q_2\ge t,\cdots ,q_k\ge t$. Let m be the largest of $q_1,q_2,\cdots ,q_k$· Show that

$$r_t(m,m,\cdots ,m)\ge r_t(q_1,q_2,\cdots ,q_k)$$

Conclude that, to prove Ramsey's theorem, it is enough to prove it in the case that $q_1=q_2=\cdots =q_k$.

设$N=r_t(m,m,\cdots ,m)$， 对于$K_N$考虑所有的 t 元素子集着色，一定存在$C_i,1\le i\le k$色的$K_m^t$。

$$K_N^t\to K_m^t,K_m^t,\cdots ,K_m^t$$

又因为$m=max\{q_1,q_2,\cdots ,q_k\}$， 那一定在每种颜色的$K_m^t$中找到该颜色的$K_{q_i}^t$，也即，

$$K_N^t\to K_{q_1}^t,K_{q_2}^t,\cdots ,K_{q_k}^t$$

得$r_t(q_1,q_2,\cdots ,q_k)\le N=r_t(m,m,\cdots ,m)$，QED。

EX26

Suppose that the mn people of a marching band are standing in a rectangular formation of m rows and n columns in such a way that in each row each person is taller than the one to his or her left. Suppose that the leader rearranges the people in each column in increasing order of height from front to back. Show that the rows are still arranged in increasing order of height from left to right.

从队列中取第 j 列和第 j+1 列进行分析，$j=1,2,\cdots ,n-1$， 记每个位置的身高为$d_{i,j}$， 初始时总有$d_{i,j}<d_{i,j+1}$。

并且定义**匹配（match）**状态为：重拍前两人站在同一行则是匹配状态。

假设重排后第 i 行不满足结论，即有$d_{i,j}\ge d_{i,j+1}$。

此外，可知第 j 列且在第 i 行后面的人一定不矮于第 i 行， $d_{x,j}\ge d_{i,j}\ge d_{i,j+1},x=i+1,\cdots ,m$， 第 j+1 列且在第 i 行前的人一定不高于第 i 行， $d_{y,j+1}\le d_{i,j+1}\le d_{i,j}，y=1,2,\cdots ,i$。 那么此时可知，第 j 列的第 i 行到第 m 行一定无法与第 j+1 列第 1 行到第 i 行形成匹配状态（匹配要满足小于而不是小于等于）， 则最多只可能是第 j 列的第 1 行到第 i-1 行与第 j+1 列的第 1 行到第 i 行形成匹配状态， 但这违反鸽巢原理（第 j+1 列有两人与第 j 列同一人形成匹配状态），因此假设不成立。

EX26PS

答案看着比较短小，但总觉得不是很通顺，感觉如果考这题会很考验语言能力。

答案的大致意思是，左侧后面的人比右侧前面的人高（应该说不比他们矮），那么这些人一定不是右侧那些人曾经的匹配对象（右侧的匹配对象一定要高于左侧），那么右侧前 i 行人只能从左侧前 i-1 行找匹配对象，这样匹配对象就不唯一了。

画图更直观一些。

EX27

A collection of subsets of {1, 2, ... ,n} has the property that each pair of subsets has at least one element in common. Prove that there are at most $2^{n-1}$ subsets in the collection.

设有 k 个不同子集$s_1,s_2,\cdots ,s_k$满足题目要求，两两集合总能找到共同元素。 那么这 k 个子集的补集$\overline{s_1},\overline{s_2},\cdots ,\overline{s_k}$也各不相同， 也不会有$s_1,s_2,\cdots s_k$中的共同元素，那么此时一共有 2k 个不同集合， 集合的数量不会超过原集合的子集总数$2^n$，所以有$2k\le 2^n\Rightarrow k\le 2^{n-1}$，QED。

EX27PS

中文翻译有些歧义，求{1, 2, ... ,n}满足要求的子集构成的集合，最多有$2^{n-1}$个元素（这里的元素是集合）。

EX28

At a dance party there are 100 men and 20 women. For each i from 1, 2, ... , 100, the ith man selects a group of $a_i$ women as potential dance partners (his "dance list," if you will), but in such a way that given any group of 20 men, it is always possible to pair the 20 men with the 20 women, with each man paired with a woman on his dance list. What is the smallest sum $a_1+a_2+\cdots +a_{100}$ for which there is a selection of dance lists that will guarantee this?

对于第 j 位女士，设$b_j$表示她出现在 100 位男士的舞伴列表中的总次数，显然有${\displaystyle \sum _{i=1}^{100}{a}_i=\sum _{j=1}^{20}{b}_j}$。

若${\displaystyle \sum _{j=1}^{20}{b}_j<1620}$，则${\displaystyle \lfloor \sum _{j=1}^{20}{b}_j/20\rfloor \le 80}$，由鸽巢原理加强版即存在$b_k\le 80$，那么可以找到 20 位男士，他们的舞伴列表中没有第 k 位女士，不符合题目要求。因此必须满足，${\displaystyle \sum _{j=1}^{20}{b}_j\ge 1620}$。

下证存在${\displaystyle \sum _{i=1}^{100}{a}_i=1620}$组成一组合理的解。

对于前 20 位男士，第 i 位男士只选择第 i 位女士，$a_i=1,i=1,2,\cdots 20$；后面的 80 位男士的舞伴列表选择全部女士，$a_i=20,i=21,22,\cdots ,100$。此时有，

$$\sum _{i=1}^{100}{a}_i=20\times 1+80\times 20=1620$$

并且任意选出 20 位男士都可以找到舞伴。

EX29

A number of different objects have been distributed into n boxes $B_1,B_2,\cdots ,B_n$. All the objects from these boxes are removed and redistributed into n + 1 new boxes $B_1^{\ast },B_2^{\ast },\cdots ,B_{n+1}^{\ast }$, with no new box empty (so the total number of objects must be at least n + 1). Prove that there are two objects each of which has the property that it is in a new box that contains fewer objects than the old box that contained it.

把新盒子与旧盒子均按递增排列，并且由题意知新盒子非空，旧盒子可能为空，确定下界。

$$0\le |B_1|\le |B_2|\le \cdots \le |B_n|,1\le |B_1^{\ast }|\le |B_2^{\ast }|\le \cdots \le |B_n^{\ast }|\le |B_{n+1}^{\ast }|$$

新旧盒子中的对象数量相等，因此不妨设$N={\displaystyle \sum _{i=1}^n|B_i|=\sum _{i=1}^{n+1}|B_i^{\ast }|}$。定义函数，

$${\mathrm{\Delta }}_i=N=\sum _{j=0}^{i+1}|B_j^{\ast }|-\sum _{j=1}^i|B_j|$$

显然，我们有两个边界值${\mathrm{\Delta }}_0=|B_1^{\ast }|\ge 1,{\mathrm{\Delta }}_N={\displaystyle \sum _{i=1}^{n+1}|B_i^{\ast }|-\sum _{i=1}^n|B_i|=0}$。

在数列中总能找到 r，满足${\mathrm{\Delta }}_{r-1}>0,{\mathrm{\Delta }}_r\le 0$， 因此，有${\mathrm{\Delta }}_{r-1}-{\mathrm{\Delta }}_r=|B_r|-|B_{r+1}^{\ast }|>0$， 进一步，有$|B_r|>|B_{r+1}^{\ast }|$，结合上面的递增序列有，

$$|B_1^{\ast }|\le |B_2^{\ast }|\le \cdots \le |B_{r+1}^{\ast }|<|B_r|\le |B_{r+1}|\le \cdots \le |B_n|$$

目前已证明了当$1\le i\le r+1,r\le j\le n$时，存在新盒子中的对象数量小于旧盒子中的对象数量，即$|B_i^{\ast }|<|B_j|$，之后定义$\theta$集合（元素满足条件：所在新盒子对象数小于旧盒子对象数），

$$\theta =(B_1^{\ast }\cup B_2^{\ast }\cup \cdots \cup B_{r+1}^{\ast })\cap (B_r\cup B_{r+1}\cup \cdots \cup B_n)$$

下证，$|\theta |\ge 2$，即满足上述不等式的对象个数不小于 2 个。仍然考虑使用${\mathrm{\Delta }}_{r-1}>0$，

$$\begin{array}{rl}|B_1^{\ast }|+|B_2^{\ast }|+\cdots +|B_r^{\ast }|>& |B_1|+|B_2|+\cdots +|B_{r-1}|\\ =& |B_1\cup B_2\cup \cdots \cup B_{r-1}|\\ \ge & |(B_1\cup B_2\cup \cdots \cup B_{r-1})\cap (B_1^{\ast }\cup B_2^{\ast }\cup \cdots \cup B_{r+1}^{\ast })|\\ =& |(B_1^{\ast }\cup B_2^{\ast }\cup \cdots \cup B_{r+1}^{\ast })\cap (U-(B_r\cup B_{r+1}\cup \cdots \cup B_n))|\\ =& |(B_1^{\ast }\cup B_2^{\ast }\cup \cdots \cup B_{r+1}^{\ast })-\theta |\\ =& |B_1^{\ast }|+|B_2^{\ast }|+\cdots +|B_{r+1}^{\ast }|-|\theta |\\ \ge & |B_1^{\ast }|+|B_2^{\ast }|+\cdots +|B_r^{\ast }|+1-|\theta |\end{array}$$

此时，必须满足$1-|\theta |<0$，并且$|\theta |$取整数，所以$|\theta |\ge 2$，QED。