第 8 章特殊计数序列

EX1

Let 2n (equally spaced) points on a circle be chosen. Show that the number of ways to join these points in pairs, so that the resulting n line segments do not intersect, equals the nth Catalan number $C_{n}$ .

EX1

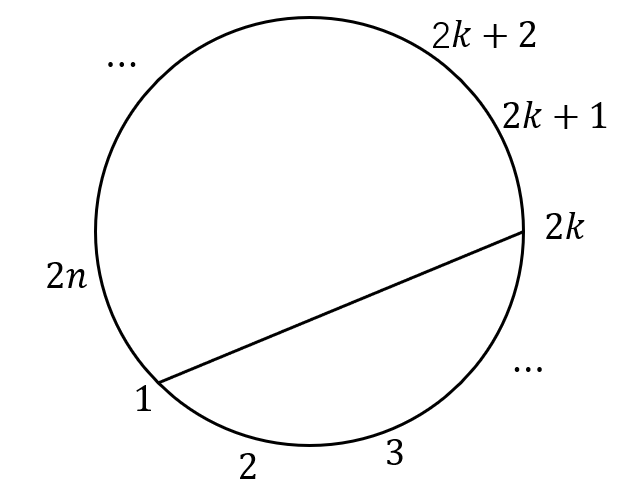
记该问题的解为 $h_{n}$ ，选择一端固定在 1 上的线段为基线，另一端指向 2k，圆上的 2n 个点被分为两组，一组有 2k-2 个，另一组有 2n-2k 个，同时问题 $h_{n}$ 被划分为 $h_{k - 1}$ 和 $h_{n - k}$ 。所以有，

h_{n} = \sum_{k = 1}^{n} h_{k - 1} h_{n - k}, n \geq 1, h_{0} = h_{1} = 1

显然 $h_{n}$ 与卡特兰数 $C_{n}$ 有相同的递推关系和初始项，因此，

h_{n} = \frac{1}{n + 1} (\binom{2 n}{n})

信息

本题与第 7 章 EX41 是类似的问题

EX2

Prove that the number of 2-by-n arrays
$\begin{matrix} x_{11} & x_{12} & \dots & x_{1 n} \\ x_{21} & x_{22} & \dots & x_{2 n} \end{matrix}$
that can be made from the numbers 1,2, ..., 2n such that
$x_{11} \leq x_{12} \leq \dots \leq x_{1 n} x_{21} \leq x_{22} \leq \dots \leq x_{2 n}$ $x_{11} \leq x_{21}, x_{12} x_{22}, . . ., x_{1 n} \leq x_{2 n}$
equals the $n$ th Catalan number, $C_{n}$ .

将数组第一行的元素标记为 +1，第二行元素标记为 -1。问题可以转化为：将 +1 和 -1 按照从左到右的顺序排列，并且保证第 i 个 +1 在第 i 个 -1 前面，即 $x_{1 i} \leq x_{2 i}$ （ $1 \leq i \leq n$ ）。

这与前 k 项和满足

a_{1} + a_{2} + \dots + a_{k} \geq 0

等价，该问题与卡特兰数的组合意义相同，解即为第 n 个卡特兰数。

EX3

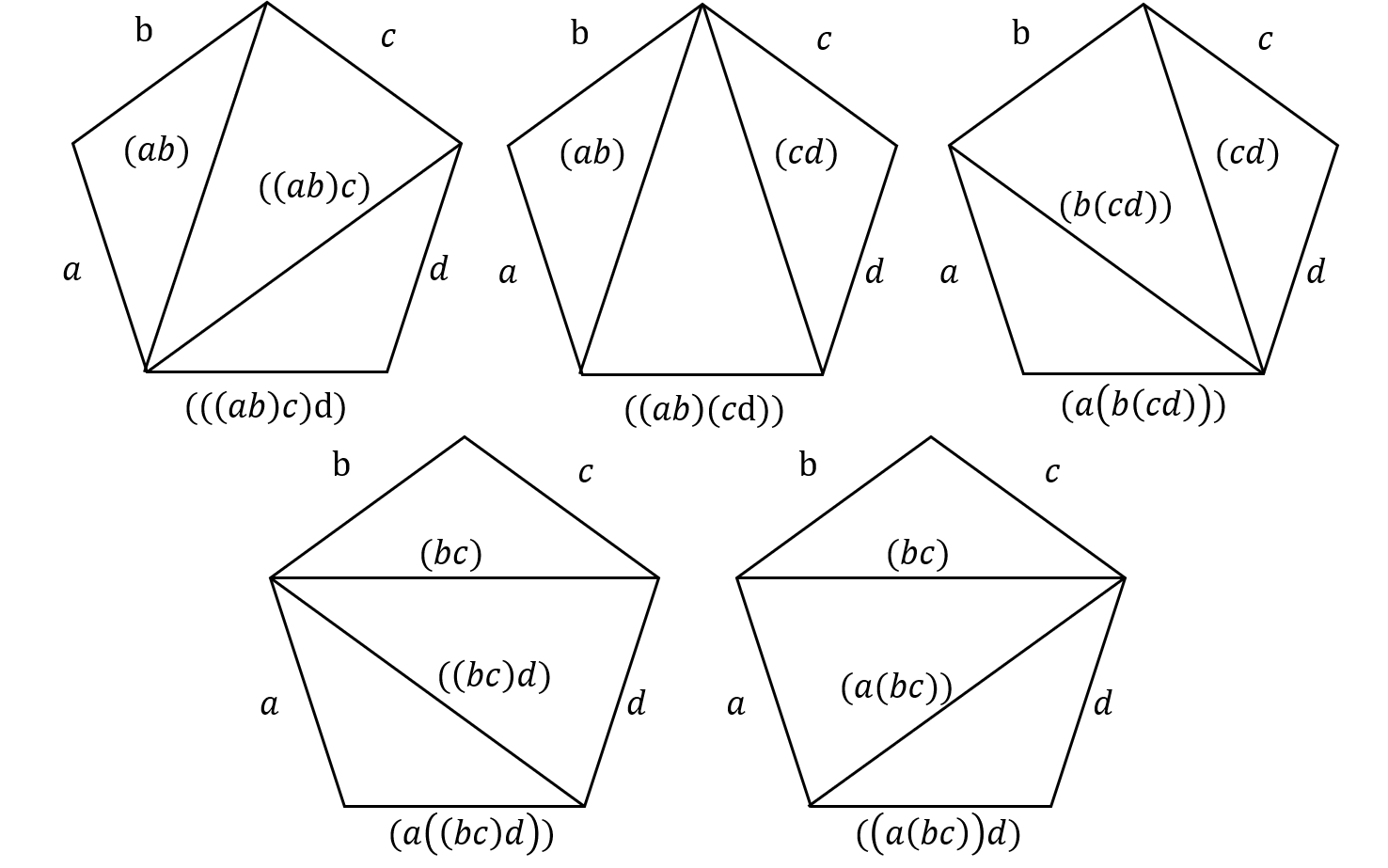
Write out all of the multiplication schemes for four numbers and the triangularization of a convex polygonal region of five sides corresponding to them.

考虑固定顺序的乘法，因此一共有 $C_{n - 1} = C_{3} = \frac{1}{4} (\binom{6}{3}) = 5$ 种方案，与之对应的三角形划分如图所示。

EX3

EX4

Determine the triangularization of a convex polygonal region corresponding to the following multiplication schemes:
(a) $(a_{1} \times (((a_{2} \times a_{3}) \times (a_{4} \times a_{5})) \times a_{6}))$
(b) $(((a_{1} \times a_{2}) \times (a_{3} \times (a_{4} \times a_{5}))) \times ((a_{6} \times a_{7}) \times a_{8}))$

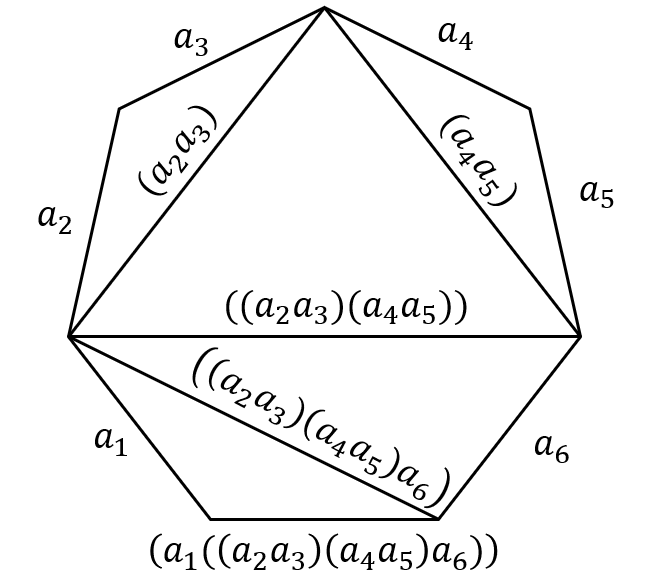
EX4(a)

以 EX4(a) 为例，步骤同上一题，

EX4

EX5 ⭐

* Let m and n be nonnegative integers with n $\leq$ m. There are m + n people in line to get into a theater for which admission is 50 cents. Of the m + n people, n have a 50-cent piece and m have a $1 dollar bill. The box office opens with an empty cash register. Show that the number of ways the people can line up so that change is available when needed is
$\frac{n - m + 1}{n + 1} (\binom{m + n}{m})$
(The case m = n is the case treated in Section 8.1.)

EX6

Let the sequence $h_{0}, h_{1}, . . ., h_{n}, \dots$ be defined by $h_{n} = 2 n^{2} - n + 3, (n \geq 0)$ . Determine the difference table, and find a formula for $\sum_{k = 0}^{n} h_{k}$ .

$h_{n}$ 是 2 次多项式，因此有 $Δ^{3} h_{n} = 0$ ，

计算 $h_{0} = 3, h_{1} = 4, h_{2} = 9$ ，一阶差分 $Δ^{1} h_{0} = 1, Δ^{1} h_{1} = 5$ , 二阶差分 $Δ^{2} h_{0} = 4$ ，即得到第 0 条对角线。

\begin{array}{cccc} 3 & 4 & 9 & \dots \\ 1 & 5 & 9 & \dots \\ 4 & 4 & 4 & \dots \\ 0 & 0 & 0 & \dots \end{array}

所以 $h_{n} = 3 (\binom{n}{0}) + (\binom{n}{1}) + 4 (\binom{n}{2})$ ，进而

\begin{aligned} \sum_{k = 0}^{n} h_{k} = & 3 \sum_{k = 0}^{n} (\binom{k}{0}) + \sum_{k = 0}^{n} (\binom{k}{1}) + 4 \sum_{k = 0}^{n} (\binom{k}{2}) \\ = & 3 (\binom{n + 1}{1}) + (\binom{n + 1}{2}) + 4 (\binom{n + 1}{3}) n \geq 0 \end{aligned}

EX7

The general term $h_{n}$ of a sequence is a polynomial in n of degree 3. If the first four entries of the Oth row of its difference table are 1, -1, 3, 10, determine $h_{n}$ and a formula for $\sum_{k = 0}^{n} h_{k}$ ·

由题意， $h_{n}$ 是 3 次多项式，那么 $Δ^{4} h_{n} = 0$ ，求出差分表第 0 条对角线，

\begin{array}{ccccc} 1 & - 1 & 3 & 10 & \dots \\ - 2 & 4 & 7 & \dots \\ 6 & 3 & \dots \\ - 3 & \dots \\ 0 & \dots \end{array}

因此 $h_{n} = (\binom{n}{0}) - 2 (\binom{n}{1}) + 6 (\binom{n}{2}) - 3 (\binom{n}{3})$ ，进而

\begin{aligned} \sum_{k = 0}^{n} h_{k} = & \sum_{k = 0}^{n} (\binom{k}{0}) - 2 \sum_{k = 0}^{n} (\binom{k}{1}) + 6 \sum_{k = 0}^{n} (\binom{k}{2}) - 3 \sum_{k = 0}^{n} (\binom{k}{3}) \\ = & (\binom{n + 1}{1}) - 2 (\binom{n + 1}{2}) + 6 (\binom{n + 1}{3}) - 3 (\binom{n + 1}{4}) n \geq 0 \end{aligned}

EX8

Find the sum of the fifth powers of the first n positive integers.

设 $h_{n} = n^{5}$ ，那么它的六阶差分为 0，求出差分表，

\begin{array}{ccccc} 0 & 1 & 32 & 243 & 1024 & 3125 \dots \\ 1 & 31 & 211 & 781 & 2101 \dots \\ 30 & 180 & 570 & 1320 & \dots \\ 150 & 390 & 750 & \dots \\ 240 & 360 & \dots \\ 120 & \dots \\ 0 & \dots \end{array}

k^{5} = (\binom{k}{1}) + 30 (\binom{k}{2}) + 150 (\binom{k}{3}) + 240 (\binom{k}{4}) + 120 (\binom{k}{5})

\begin{aligned} \sum_{k = 1}^{n} k^{5} = & \sum_{k = 1}^{n} (\binom{k}{1}) + 30 \sum_{k = 1}^{n} (\binom{k}{2}) + 150 \sum_{k = 0}^{n} (\binom{k}{3}) + 240 \sum_{k = 0}^{n} (\binom{k}{4}) + 120 \sum_{k = 0}^{n} (\binom{k}{5}) \\ = & (\binom{n + 1}{2}) + 30 (\binom{n + 1}{3}) + 150 (\binom{n + 1}{4}) + 240 (\binom{n + 1}{5}) + 120 (\binom{n + 1}{6}) \end{aligned}

EX9

Prove that the following formula holds for the kth-order differences of a sequence $h_{0}, h_{1}, \dots, h_{n}, \dots$ :
$Δ^{k} h_{n} = \sum_{j = 0}^{k} (- 1)^{k - j} (\binom{k}{j}) h_{n + j}$

采用数学归纳法证明，当 k=0 时，有

Δ h_{n} = (- 1)^{0} (\binom{0}{0}) h_{0} = h_{0}

成立，假设当 $k = m$ 时结论成立，即有

Δ^{m} h_{n} = \sum_{j = 0}^{m} (- 1)^{m - j} (\binom{m}{j}) h_{n + j}

当 $k = m + 1$ 时，

\begin{aligned} Δ^{m + 1} h_{n} = & Δ^{m} h_{n + 1} - Δ^{m} h_{n} \\ = & \sum_{j = 0}^{m} (- 1)^{m - j} (\binom{m}{j}) h_{n + 1 + j} - \sum_{j = 0}^{m} (- 1)^{m - j} (\binom{m}{j}) h_{n + j} \\ = & \sum_{j = 1}^{m + 1} (- 1)^{m - j + 1} (\binom{m}{j - 1}) h_{n + j} - \sum_{j = 0}^{m} (- 1)^{m - j} (\binom{m}{j}) h_{n + j} \\ = & (h_{n + (m + 1)} - (- 1)^{m} h_{n}) + \sum_{j = 1}^{m} ((- 1)^{m - j + 1} (\binom{m}{j - 1}) - (- 1)^{m - j} (\binom{m}{j})) h_{n + j} \\ = & (- 1)^{(m + 1) - (m + 1)} h_{n + (m + 1)} + (- 1)^{(m + 1) - 0} h_{n + 0} + \sum_{j = 1}^{m} ((- 1)^{m + 1 - j} (\binom{m}{j - 1}) + (- 1)^{m + 1 - j} (\binom{m}{j})) h_{n + j} \\ = & (- 1)^{(m + 1) - (m + 1)} h_{n + (m + 1)} + (- 1)^{(m + 1) - 0} h_{n + 0} + \sum_{j = 1}^{m} (- 1)^{m + 1 - j} (\binom{m + 1}{j})) h_{n + j} \\ = & \sum_{j = 0}^{m + 1} (- 1)^{m + 1 - j} (\binom{m + 1}{j}) h_{n + j} \end{aligned}

综上，证毕。

EX10

If $h_{n}$ is a polynomial in n of degree m, prove that the constants $c_{0}, c_{1}, \dots, c_{m}$ such that
$h_{n} = c_{0} (\binom{n}{0}) + c_{1} (\binom{n}{1}) + \dots + c_{m} (\binom{n}{m})$
are uniquely determined. (Cf. Theorem 8.2.2.)

本题主要证明唯一性，假设存在不同的序列 ${c_{i}}_{i = 0}^{m}$ 和序列 ${d_{i}}_{i = 0}^{m}$ 使得存在 i 满足 $c_{i} \neq d_{i}$ ，其中 $0 \leq i \leq m$ ，

\begin{aligned} h_{n} = & c_{0} (\binom{n}{0}) + c_{1} (\binom{n}{1}) + \dots + c_{m} (\binom{n}{m}) \\ = & d_{0} (\binom{n}{0}) + d_{1} (\binom{n}{1}) + \dots + d_{m} (\binom{n}{m}) \end{aligned}

\sum_{k = 0}^{m} (c_{k} - d_{k}) (\binom{n}{k}) = 0

显然 $(\binom{n}{k}) > 0$ ，那么只能是 $c_{k} - d_{k} = 0, 0 \leq k \leq m$ ，这与假设矛盾，因此假设不成立。

EX11

Compute the Stirling numbers of the second kind S(8, k), (k = 0, 1, ..., 8).

第二类 Stirling 数的性质，

$S (p, 0) = 0, p \geq 1$
$S (p, p) = 1, p \geq 0$
$S (p, k) = k S (p - 1, k) + S (p - 1, k - 1)$

进行打表，

$k$	0	1	2	3	4	5	6	7	8
$S (8, k)$	0	1	127	966	1701	1050	266	28	1

验证程序

cpp

 #include <iostream>
#include <vector>

using namespace std;
int main() {
    auto stirList = vector<vector<int>>(10, vector<int>(10, 0));
    for(int p = 1; p < 10; ++ p) {
        stirList[p][p] = 1;
    }
    for(int p = 2; p < 10; ++ p) {
        for(int k = 1; k < p; ++ k) {
            stirList[p][k] = stirList[p-1][k] * k + stirList[p-1][k-1];
        }
    }
    for(int p = 0; p < 10; ++ p) {
        for(int k = 0; k <= p; ++ k) {
            printf("%d\t", stirList[p][k]);
        }
        printf("\n");
    }

    printf("\n S(8, k), k = 0, 1, 2, ..., 8\n");
    for(int k = 0; k <= 8; ++ k) {
        printf("%d\t", stirList[8][k]);
    }
    return 0;
}

EX12

Prove that the Stirling numbers of the second kind satisfy the following relations:
(a) $S (n, 1) = 1, (n \geq 1)$
(b) $S (n, 2) = 2^{n - 1} - 1, (n \geq 2)$
(c) $S (n, n - 1) = (\binom{n}{n}), (n \geq 1)$
(d) $S (n, n - 2) = (\binom{n}{3}) + 3 (\binom{n}{4}) (n \geq 2)$

EX12(a)

由定理 8.2.5 知 $S (p, k)$ 是把 p 个元素集合划分到 k 个不可区分的盒子且没有空盒子的划分个数。因此， $S (p, 1)$ 是把 p 个元素划分到 1 个盒子且没有空盒子的划分个数，显然只有 1 种。

EX12(b)

S (p, p) = 1, S (p, 1) = 1

\begin{aligned} S (n, 2) = & 2 S (n - 1, 2) + S (n - 1, 1) \\ = & 2 S (n - 1, 2) + 1 \\ = & 2 (2 S (n - 2, 2) + S (n - 2, 1)) + 1 \\ = & 2^{2} S (n - 2, 2) + (1 + 2) \\ = & 2^{3} S (n - 3, 2) + (1 + 2 + 2^{2}) \\ = & \dots \\ = & 2^{n - 2} S (n - (n - 2), 2) + (1 + 2 + 2^{2} + \dots + 2^{n - 3}) \\ = & \frac{1 - 2^{n - 1}}{1 - 2} \\ = & 2^{n - 1} - 1 \end{aligned}

EX12(c)

使用数学归纳法证明，当 n=1 时， $S (1, 0) = 0 = (\binom{1}{2})$ ，显然成立。假设当 $n = k$ 时有 $S (k, k - 1) = (\binom{k}{2})$ ，当 $n = k + 1$ 时有，

\begin{aligned} S (k + 1, k) = & k S (k, k) + S (k, k - 1) \\ = k + (\binom{k}{2}) \\ = k + \frac{k (k - 1)}{2} \\ = \frac{k (k + 1)}{2} \\ = (\binom{k + 1}{2}) \end{aligned}

综上，证毕。

EX12(d)

考虑问题：将 n 个元素划分到 n-2 个不可区分的盒子且没有空盒子的个数 S(n, n-2)。

如果有一个盒子中有三个元素，有 $(\binom{n}{3})$ 种情况；如果有两个盒子各有两个元素，先从 n 个元素中选出 2 个，再从剩余 n-2 个元素中选出 2 个，两种情况对称，因此是 $\frac{(\binom{n}{2}) (\binom{n - 2}{2})}{2!} = 3 (\binom{n}{4})$ 。

因此有 $S (n, n - 2) = (\binom{n}{3}) + 3 (\binom{n}{4})$ 。

EX13

Let X be a p-element set and let Y be a k-element set. Prove that the number of functions $f : X \to Y$ which map X onto Y equals
$k! S (p, k) = S^{♯} (p, k)$

X 映射到 Y 是满射，映射函数等价于把 p 个元素放入到 k 个可区分的盒子中，即有 $S^{♯} (p, k)$ 个；同时由可区分盒子与不可区分盒子划分的关系，有 $S^{♯} (p, k) = k! S (p, k)$ ，因此映射函数的个数也等于 $k! S (p, k)$ 。

翻译错误

中文版中满射（onto）被错译成到上函数

EX14 ⭐

* Find and verify a general formula for
$\sum_{k = 0}^{n} k^{p}$
involving Stirling numbers of the second kind.

EX15

The number of partitions of a set of n elements into k distinguishable boxes (some of which may be empty) is $k_{n}$ . By counting in a different way, prove that
$k^{n} = (\binom{k}{1}) 1! S (n, 1) + (\binom{k}{2}) 2! S (n, 2) + \dots + (\binom{k}{n}) n! S (n, n)$
If $k \geq n$ , define $S (n, k)$ to be 0.

方法一：考虑把 n 个元素分别放在 k 个盒子中，每个元素有 k 种放置放法，因此共 $k^{n}$ 种方法。

方法二：先区分盒子是否非空，从 k 个盒子中选出 i 个非空盒子，问题变为把 n 个元素放入 i 个可区分盒子且盒子非空中的方法数，即为 $S^{♯} (n, i)$ ，i 可能的取值为 $i = 1, 2, \dots, k$ ，

\sum_{i = 1}^{k} (\binom{k}{i}) S^{♯} (n, i) = \sum_{i = 1}^{k} (\binom{k}{i}) i! S (n, i)

方法一和方法二是同一问题的两种解决方法，因此等价，所以有，

k^{n} = (\binom{k}{1}) 1! S (n, 1) + (\binom{k}{2}) 2! S (n, 2) + \dots + (\binom{k}{n}) n! S (n, n)

翻译错误

本题中文书中有翻译错误，把可区分写成了不可区分。

EX16

Compute the Bell number $B_{8}$ . (Cf. Exercise 11.)

Bell 数 $B_{p}$ 是第 p 行的第二类 Stirling 数 $S (p, k)$ 之和。

0 + 1 + 127 + 966 + 1701 + 1050 + 266 + 28 + 1 = 4140

程序验证

cpp

#include <iostream>
#include <vector>

using namespace std;
int main() {
    auto stirList = vector<vector<int>>(10, vector<int>(10, 0));
    for(int p = 1; p < 10; ++ p) {
        stirList[p][p] = 1;
    }
    for(int p = 2; p < 10; ++ p) {
        for(int k = 1; k < p; ++ k) {
            stirList[p][k] = stirList[p-1][k] * k + stirList[p-1][k-1];
        }
    }
    for(int p = 0; p < 10; ++ p) {
        for(int k = 0; k <= p; ++ k) {
            printf("%d\t", stirList[p][k]);
        }
        printf("\n");
    }

    printf("\n S(8, k), k = 0, 1, 2, ..., 8\n");
    int bellNum = 0;
    for(int k = 0; k <= 8; ++ k) {
        printf("%d\t", stirList[8][k]);
        bellNum += stirList[8][k];
    }
    printf("\n Bell number B8 is %d\n", bellNum);
    return 0;
}

EX17

Compute the triangle of Stirling numbers of the first kind s(n, k) up to n = 7.

第一类 Stirling 数的递推关系为，

s (p, k) = (p - 1) s (p - 1, k) + s (p - 1, k - 1)

初始条件与第二类 Stirling 数相同， $s (p, p) = 1, s (p, 0) = 0, p \geq 1, s (0, 0) = 1$ 。

程序验证

cpp

#include <iostream>
#include <vector>

using namespace std;
int main() {
    auto firstStirList = vector<vector<int>>(10, vector<int>(10, 0));
    for(int p = 1; p < 10; ++ p) {
        firstStirList[p][p] = 1;
    }
    for(int p = 2; p < 10; ++ p) {
        for(int k = 1; k < p; ++ k) {
            firstStirList[p][k] = firstStirList[p-1][k] * (p-1)
                                + firstStirList[p-1][k-1];
        }
    }
    for(int p = 0; p < 10; ++ p) {
        for(int k = 0; k <= p; ++ k) {
            printf("%d\t", firstStirList[p][k]);
        }
        printf("\n");
    }

    printf("\n s(7, k), k = 0, 1, 2, ..., 7\n");
    for(int k = 0; k <= 7; ++ k) {
        printf("%d\t", firstStirList[7][k]);
    }
    return 0;
}

EX18

Write $[n]_{k}$ as a polynomial in n for k = 5,6, and 7.

由定义可以求出 $[n]_{5}$ ，

\begin{aligned} _{5} = & n (n - 1) (n - 2) (n - 3) (n - 4) \\ = & n^{5} - 10 n^{4} + 35 n^{3} - 50 n^{2} + 24 n \end{aligned}

也可以通过查表写 $[n]_{7}$ ，

\begin{aligned} _{7} = & \sum_{k = 0}^{7} (- 1)^{7 - k} s (7, k) n^{k} \\ = & n^{7} - 21 n^{6} + 175 n^{5} - 735 n^{4} + 1624 n^{3} - 1764 n^{2} + 720 n \end{aligned}

EX19 👻

Prove that the Stirling numbers of the first kind satisfy the following formulas:
(a) $s (n, 1) = (n - 1)!, (n \geq 1)$
(b) $s (n, n - 1) = (\binom{n}{2}), (n \geq 1)$

结合递归式，易证。

EX20

VerifY that $[n]_{n}$ = n!, and write n! as a polynomial in n using the Stirling numbers of the first kind. Do this explicitly for n = 6.

$[n]_{p}$ 的定义形式 $[n]_{p} = n (n - 1) (n - 2) \dots (n - (p - 1)), p \geq 1$ ，当 n=0 时， $[n]_{0} = 1$ 。

带入 $p = n$ 显然有 $[n]_{n} = n!, n \geq 0$ 。

$[n]_{p}$ 与第一类 Stirling 数的关系， $[n]_{p} = \sum_{k = 0}^{p} (- 1)^{k - p} s (p, k) n^{k}$ ，

带入 $p = n$ 有，

n! = [n]_{n} = \sum_{k = 0}^{n} (- 1)^{n - k} s (p, k) n^{k}

当 $n = 6$ 时，结合 s(p, k) 三角形有，

6! = 6^{6} - 15 \times 6^{5} + 85 \times 6^{4} - 225 \times 6^{3} + 274 \times 6^{2} - 120 \times 6^{1} + 0 \times 6^{0}

EX21

For each integer n = 1,2,3,4,5, construct the diagram of the set $P_{n}$ of partitions of n, partially ordered by majorization.

~~这里的图（diagram）指的是 Ferrers 图，这是很容易画出的，以 $5 = 4 + 1$ 为例，~~

EX21

信息

本题应该是优超（majorize）关系的 Hasse 图。

EX22 👻

(a) Calculate the partition number $p_{6}$ and construct the diagram of the set $P_{6}$ , partially ordered by majorization.
(b) Calculate the partition number $p_{7}$ and construct the diagram of the set $P_{7}$ , partially ordered by majorization.

EX22(a)

以 (a) 为例，6 对应的分拆为，

6, 51, 42, 411, 33, 321, 3111, 222, 2211, 21111, 111111

因此 $p_{6} = 11$ 。

EX23

A total order on a finite set has a unique maximal element (a largest element) and a unique minimal element (a smallest element). What are the largest partition and smallest partition in the lexicographic order on $P_{n}$ (a total order)?

最大分拆为 n，最小分拆为 $n = 1 + 1 + \dots + 1$ 。

EX24 🚧

A partial order on a finite set may have many maximal elements and minimal elements. In the set $P_{n}$ of partitions of n partially ordered by majorization, prove that there is a unique maximal element and a unique minimal element.

简评

看了几份答案，似乎都不是严格的证明，只是稍微解释了 $n$ 比其它都大， $\underset{n 个}{\underset{⏟}{1 + 1 + \dots + 1}}$ 比其它都小。

待完善

EX25

Let $t_{1}, t_{2}, \dots, t_{m}$ be distinct positive integers, and let
$q_{n} = q_{n} (t_{1}, t_{2}, \dots, t_{m})$
equal the number of partitions of n in which all parts are taken from $t_{1}, t_{2}, \dots, t_{m}$ . Define $q_{0} = 1$ . Show that the generating function for $q_{0}, q_{1}, \dots, q_{n}, \dots$ is
$\prod_{k = 1}^{m} (1 - x^{t_{k}})^{- 1}$

\begin{aligned} \prod_{k = 1}^{m} (1 - x^{t_{k}})^{- 1} = & \frac{1}{1 - x^{t_{1}}} \frac{1}{1 - x^{t_{2}}} \dots \frac{1}{1 - x^{t_{m}}} \\ = & (\sum_{n_{1} = 0}^{\infty} x^{t_{1} n_{1}}) (\sum_{n_{2} = 0}^{\infty} x^{t_{2} n_{2}}) \dots (\sum_{n_{m} = 0}^{\infty} x^{t_{m} n_{m}}) \\ = & \sum_{n_{1} = 0}^{\infty} \sum_{n_{2} = 0}^{\infty} \dots \sum_{n_{m} = 0}^{\infty} x^{n_{1} t_{1} + n_{2} t_{2} \dots + n_{m} t_{m}} \\ = & \sum_{n = 0}^{\infty} q_{n} x^{n} \end{aligned}

由分拆数的性质， $q_{n}$ 等于方程 $n_{1} t_{1} + n_{2} t_{2} + \dots + n_{m} t_{m} = n$ 非负整数解 $n_{1}, n_{2}, \dots, n_{m}$ 的个数，所以 $q_{0}, q_{1}, \dots, q_{n}, \dots$ 的生成函数为

\prod_{k = 1}^{m} (1 - x^{t_{k}})^{k}

EX26 👻

Determine the conjugate of each of the following partitions:
(a) $12 = 5 + 4 + 2 + 1$
(b) $15 = 6 + 4 + 3 + 1 + 1$
(c) $20 = 6 + 6 + 4 + 4$
(d) $21 = 6 + 5 + 4 + 3 + 2 + 1$
(e) $29 = 8 + 6 + 6 + 4 + 3 + 2$

EX26(a)

以 (a) 为例，先画出 Ferrrers 图，再画出共轭分拆的图，

EX26

因此共轭分拆为 $12 = 4 + 3 + 2 + 2 + 1$ 。

EX27

For each integer n > 2, determine a self-conjugate partition of n that has at least two parts.

设 $λ$ 是 n 的分拆 $n_{1} + n_{2} + \dots + n_{k}$ ，当 n 为奇数时，取 $n_{1} = \frac{(n + 1)}{2}, n_{2} = n_{3} = \dots = n_{k} = 1, k = \frac{n + 1}{2}$ 。

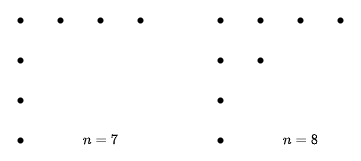
当 n 为偶数时，取 $n_{1} = \frac{n}{2}, n_{2} = 2, n_{3} = n_{4} = \dots = n_{k} = 1, k = \frac{n}{2}$ 。

以 n=7 和 n=8 分别为奇数和偶数的例子，如图，

EX27

EX28

Prove that conjugation reverses the order of majorization; that is, if $λ$ and $μ$ are partitions of n and $λ$ is majorized by $μ$ , then $μ^{*}$ is majorized by $λ^{*}$ .

由题意，当 $λ$ 被 $μ$ 优超时，有

\begin{matrix} (1) & λ_{1} + λ_{2} + \dots + λ_{i} \leq μ_{1} + μ_{2} + μ_{i}, 1 \leq i \leq k \end{matrix}

假设 $μ^{} ≰ λ^{*}$ ，即存在 k 使，

μ_{1}^{*} + μ_{2}^{*} + \dots + μ_{i}^{*} \leq λ_{1}^{*} + λ_{2}^{*} + \dots + λ_{i}^{*}, 1 \leq i < k

μ_{1}^{*} + μ_{2}^{*} + \dots + μ_{k}^{*} > λ_{1}^{*} + λ_{2}^{*} + \dots + λ_{k}^{*}

即有 $μ_{k}^{*} > λ_{k}^{*}$ ，记 $u = μ_{k}^{*}, v = λ_{k}^{*}$ 。又因为 $μ^{*}$ 和 $λ^{*}$ 都是 n 的分拆，所以有

μ_{k + 1}^{*} + μ_{k + 2}^{*} + \dots \leq λ_{k + 1}^{*} + λ_{k + 2}^{*} + \dots

如图，由互换行列前后的关系可得，

EX28

μ_{k + 1}^{*} + μ_{k + 2}^{*} \dots = \sum_{1}^{u} (u_{i} - k), λ_{k + 1}^{*} + λ_{k + 2}^{*} + \dots = \sum_{i = 1}^{v} (λ_{i} - k)

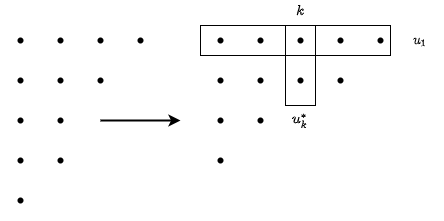
根据放缩，

\sum_{i = 1}^{v} (μ_{i} - k) < \sum_{i = 1}^{u} \leq \sum_{i = 1}^{v} (λ_{i} - k)

可得

\begin{matrix} (2) & μ_{1} + μ_{2} + \dots + μ_{v} < λ_{1} + λ_{2} + \dots + λ_{v} \end{matrix}

其中 (1) 式与 (2) 式矛盾，因此假设不成立，综上，证毕。

EX29

Prove that the number of partitions of the positive integer n into parts each of which is at most 2 equals $⌊ n / 2 ⌋ + 1$ . (Remark: There is a formula, namely the nearest integer to $\frac{(n+3)^2}{12}, for the number of partitions of n into parts each of which is at most 3 but it is much more difficult to prove. There is also one for partitions with no part more than 4, but it is even more complicated and difficult to prove.)

当 $n = 2 r$ 时，每一部分至多是 2 的分拆为

1^{n}, 2^{1} 1^{n - 2}, 2^{2} 1^{n - 4}, \dots, 2^{r}

当 $n = 2 r + 1$ 时，每一部分最多是 2 的分拆为

1^{n}, 2^{1} 1^{n - 2}, 2^{2} 1^{n - 4}, \dots, 2^{r} 1^{1}

不论奇偶，都是分拆为 r+1 个部分，当 r 为偶数时， $r + 1 = \frac{n}{2} + 1 = ⌊ n / 2 ⌋ + 1$ ，当 r 为奇数时， $r + 1 = \frac{n - 1}{2} + 1 = ⌊ (n + 1) / 2 ⌋ = ⌊ n / 2 ⌋ + 1$ 。

综上，分拆成每一部分至多是 2 的分拆数等于 $⌊ n / 2 ⌋$ 。

EX30

Prove that the partition function satisfies
$p_{n} > p_{n - 1} (n \geq 2)$

考虑 n-1 的分拆数和 n 的分拆数，显然所有 n-1 的分拆数 +1 都是 n 的分拆数，此外 n 还有它自己作为分拆数，因此一定有 $p_{n} > p_{n - 1}$ 。

EX31 🚧

Evaluate $h_{k - 1}^{(k)}$ the number of regions into which k-dimensional space is partitioned by k - 1 hyperplanes in general position.

h_{k - 1}^{(k)} = (\binom{k - 1}{0}) + (\binom{k - 1}{1}) + \dots + (\binom{k - 1}{k - 1}) + (\binom{k - 1}{k}) = 2^{k - 1}

EX32

Use the recurrence relation (8.31) to compute the small Schroder numbers $s_{8}$ and $s_{9}$ .

小 Schroder 数的性质：

$s_{1} = s_{2} = 1$
$(n + 2) s_{n + 2} - 3 (2 n + 1) x_{n + 1} + (n - 1) s_{n} = 0, n \geq 1$

由递推关系和初始项，可以计算出 $s_{3} = 3, s_{4} = 11, s_{5} = 45, s_{6} = 197, s_{7} = 903$ ，

8 s_{8} - 3 \times 13 \times 903 + 5 \times 197 = 0

求出 $s_{8} = 4279$ ，同理可以求出 $9 s_{9} - 3 \times 15 \times 4279 + 6 \times 903 = 0$ ，得 $s_{9} = 20793$ 。

EX33

Use the recurrence relation (8.32) to compute the large Schroder numbers $R_{7}$ and $R_{8}$ . Verify that $R_{7} = 2 s_{8}$ and $R_{8} = 2 s_{9}$ , as stated in Corollary 8.5.8.

大 Schroder 数的性质：

R_{n} = \sum_{r = 0}^{n} \frac{1}{n - r + 1} \frac{(2 n - r)!}{r! [(n - r)!]^{2}}

带入 $n = 7$ 计算，

\begin{aligned} R_{7} = & \sum_{r = 0}^{7} \frac{1}{8 - r} \frac{(14 - r)!}{r! [(7 - r)!]^{2}} \\ = & \frac{1}{8} \frac{14!}{0! (7!)^{2}} + \frac{1}{7} \frac{13!}{1! (6!)^{2}} + \frac{1}{6} \frac{12!}{2! (5!)^{2}} + \frac{1}{5} \frac{11!}{3! (4!)^{2}} + \frac{1}{4} \frac{10!}{4! (3!)^{2}} + \frac{1}{3} \frac{9!}{5! (2!)^{2}} + \frac{1}{2} \frac{8!}{6! (1!)^{2}} + \frac{1}{1} \frac{7!}{7! (0!)^{2}} \\ = & 8558 = 2 \times 4279 = 2 s_{8} \end{aligned}

提示

题目要求使用递推关系计算，大 Schroder 数的递推关系为，

R_{n} = R_{n - 1} + \sum_{k = 1}^{n} R_{k - 1} R_{n - k}

注意与 Catalan 数进行区分。

EX34

Use the generating function for the large Schroder numbers to compute the first few large Schroder numbers.

大 Schroder 数序列的生成函数为

\sum_{n = 0}^{\infty} R_{n} x^{n} = \frac{1}{2 x} (- (x - 1) - \sqrt{x^{2} - 6 x + 1})

$\sqrt{x^{2} - 6 x + 1}$ 在 x=0 处的泰勒级数为 $1 - 3 x - 4 x^{2} - 12 x^{3} - 44 x^{4} + \dots$ ，

因此，

\begin{aligned} \sum_{k = 0}^{\infty} R_{n} x^{n} = & \frac{1}{2 x} (- (x - 1) - (1 - 3 x - 4 x^{2} - 12 x^{3} - 44 x^{4} + \dots)) \\ = & \frac{2 x + 4 x^{2} + 12 x^{3} + 44 x^{4} + \dots}{2 x} \\ = & 1 + 2 x + 6 x^{2} + 22 x^{3} + \dots \end{aligned}

综上，有 $R_{0} = 1, R_{1} = 2, R_{2} = 6, R_{3} = 22$ 。

EX35

Use the generating function for the small Schroder numbers to compute the first few small Schroder numbers.

小 Schroder 数序列的生成函数为

\sum_{n = 1}^{\infty} s_{n} x^{n} = \frac{1}{4} (1 + x - \sqrt{x^{2} - 6 x + 1})

同上，带入 $\sqrt{x^{2} - 6 x + 1}$ 的泰勒级数，

\begin{aligned} \sum_{k = 1}^{\infty} s_{n} x^{n} = & \frac{4 x + 4 x^{2} + 12 x^{3} + 44 x^{4} + \dots}{4} \\ = & x + x^{2} + 3 x^{3} + 11 x^{4} + \dots \end{aligned}

综上，有 $r_{1} = 1, r_{2} = 1, r_{3} = 3, r_{4} = 11$ 。

EX36

Prove that the Catalan number $C_{n}$ equals the number of lattice paths from (0,0) to (2n, 0) using only upsteps (1, 1) and downsteps (1, -1) that never go above the horizontal axis (so there are as many up steps as there are downsteps). (These are sometimes called Dyck paths.)

记上行步 (1,1) 为 -1，下行步 (1,-1) 为 +1，步行序列为 $a_{1}, a_{2}, \dots, a_{2 n}$ 。

因为起点 y 坐标与终点 y 坐标相同，那么一定有 n 个上行步（+1）和 n 个下行步（-1），并且从不经过水平轴上方的格路径，即前 k 项和 $a_{1} + a_{2} + \dots + a_{k} \geq 0, 1 \leq k \leq 2 n$ ，该问题与第 n 个 Catalan 数的组合意义相同，因此等于 $C_{n}$ 。

EX37 ⭐

* The large Schroder number $C_{n}$ counts the number of subdiagonal HVD-lattice paths from (0,0) to (n, n). The small Schroder number counts the number of dissections of a convex polygonal region of n + 1. Since $R_{n} = 2 s_{n + 1}$ for n $\leq$ 1, there are as many subdiagonal HVD-lattice paths from (0,0) to (n, n) as there are dissections of a convex polygonal region of n + 1 sides. Find a one-to-one correspondence between these lattice paths and these dissections.

第 8 章 特殊计数序列 ​

EX1 ​

EX2 ​

EX3 ​

EX4 ​

EX4(a) ​

EX5 ⭐ ​

EX6 ​

EX7 ​

EX8 ​

EX9 ​

EX10 ​

EX11 ​

EX12 ​

EX12(a) ​

EX12(b) ​

EX12(c) ​

EX12(d) ​

EX13 ​

EX14 ⭐ ​

EX15 ​

EX16 ​

EX17 ​

EX18 ​

EX19 👻 ​

EX20 ​

EX21 ​

EX22 👻 ​

EX22(a) ​

EX23 ​

EX24 🚧 ​

EX25 ​

EX26 👻 ​

EX26(a) ​

EX27 ​

EX28 ​

EX29 ​

EX30 ​

EX31 🚧 ​

EX32 ​

EX33 ​

EX34 ​

EX35 ​

EX36 ​

EX37 ⭐ ​

第 8 章特殊计数序列

EX1

EX2

EX3

EX4

EX4(a)

EX5 ⭐

EX6

EX7

EX8

EX9

EX10

EX11

EX12

EX12(a)

EX12(b)

EX12(c)

EX12(d)

EX13

EX14 ⭐

EX15

EX16

EX17

EX18

EX19 👻

EX20

EX21

EX22 👻

EX22(a)

EX23

EX24 🚧

EX25

EX26 👻

EX26(a)

EX27

EX28

EX29

EX30

EX31 🚧

EX32

EX33

EX34

EX35

EX36

EX37 ⭐