第 7 章递推关系和生成函数

EX1

Let $f_{0}, f_{1}, f_{2}, . . ., f_{n}, . . .$ , denote the Fibonacci sequence. By evaluating each of the following expressions for small values of n, conjecture a general formula and then prove it, using mathematical induction and the Fibonacci recurrence:
(a) $f_{1} + f_{3} + \dots + f_{2 n - 1}$
(b) $f_{0} + f_{2} + \dots + f_{2 n}$
(c) $f_{0} - f_{1} + f_{2} - \dots + (- 1)^{n} f_{n}$
(d) $f_{0}^{2} + f_{1}^{2} + \dots + f_{n}^{2}$

EX1(a)(b)

先打表找规律，

打表程序

cpp

#include <iostream>
#include <vector>

using namespace std;

int main()
{
    int p = 0, q = 1;
    vector<int> fibList {p, q};
    for(int i = 0; i < 50; ++ i) {
        fibList.emplace_back(p+q);
        p = q;
        q = fibList.back();
    }

    int odd_total = 0, even_total = 0, alter_total = 0, square_total;
    int flag = 1;
    printf("idx \t sum_odd \t sum_total \t sum_alter \t sum_square \n");
    for(int i = 0; i < 10; ++ i) {
        odd_total += fibList[max(2*i-1, 0)];
        even_total += fibList[2*i];
        alter_total += flag * fibList[i];
        flag *= -1;
        square_total += fibList[i] * fibList[i];
        printf("%d \t %d \t %d \t %d \t %d\n", i, odd_total, even_total,
                alter_total, square_total);
    }
    return 0;
}

可以发现： $f_{1} + f_{3} + \dots + f_{2 n - 1} = f_{2 n}$ ， $f_{0} + f_{2} + \dots + f_{2 n} = f_{2 n + 1} - 1$ ， $f_{0} - f_{1} + f_{2} - \dots + (- 1)^{n} f_{n} = - 1 + (- 1)^{n} f_{n - 1}$ ， $f_{0}^{2} + f_{1}^{2} + \dots + f_{n}^{2} = f_{n} f_{n + 1}$ 。

数学归纳证明过程略。

EX1(c)

f_{0} - f_{1} + f_{2} - \dots + (- 1)^{n} f_{n} = - 1 + (- 1)^{n} f_{n - 1}, (n \geq 1)

对于特殊的 $f_{0}$ 有 $f_{0} = 0$ 。

EX1(d)

这个强调一下特殊的构造方法，辅助猜测递推公式，后面也会用到这个构造法。

\begin{aligned} \sum_{i = 0}^{n} f_{i} & = f_{0}^{2} + \sum_{i = 1}^{n} f_{i}^{2} \\ = f_{0} f_{1} + \sum_{i = 1}^{n} f_{i} (f_{i + 1} - f_{i - 1}) \\ = f_{0} f_{1} + (f_{1} f_{2} - f_{1} f_{0}) + (f_{2} f_{3} - f_{2} f_{1}) + \dots + (f_{n} f_{n + 1} - f_{n} f_{n - 1}) \\ = f_{n} f_{n + 1} \end{aligned}

EX2

Prove that the nth Fibonacci number In is the integer that is closest to the number
$\frac{1}{\sqrt{5}} {(\frac{1 + \sqrt{5}}{2})}^{n}$

设 $a = \frac{1}{\sqrt{5}} {(\frac{1 + \sqrt{5}}{2})}^{n}$ ，并且知道 $f_{n} = \frac{1}{\sqrt{5}} {(\frac{1 + \sqrt{5}}{2})}^{n} - \frac{1}{\sqrt{5}} {(\frac{1 - \sqrt{5}}{2})}^{n}$ ，那么 $f_{n}$ 与 a 的距离为，

\begin{aligned} | f_{n} - a | = & | \frac{1}{\sqrt{5}} {(\frac{1 - \sqrt{5}}{2})}^{n} | \\ = & \frac{1}{\sqrt{5}} {(\frac{(\sqrt{5} - 1) (\sqrt{5} + 1)}{2 (\sqrt{5} + 1)})}^{n} \\ = & \frac{1}{\sqrt{5}} {(\frac{2}{\sqrt{5} + 1})}^{n} \\ \leq & \frac{1}{\sqrt{5}} \frac{2}{\sqrt{5} + 1} \\ = & \frac{2}{5 + \sqrt{5}} \\ \leq & \frac{2}{5} \end{aligned}

因此， $f_{n}$ 是最接近 $\frac{1}{\sqrt{5}} {(\frac{1 + \sqrt{5}}{2})}^{n}$ 的整数。

EX3

Prove the following about the Fibonacci numbers:
(a) $f_{n}$ is even if and only if n is divisible by 3.
(b) $f_{n}$ is divisible by 3 if and only if n is divisible by 4.
(c) $f_{n}$ is divisible by 4 if and only if n is divisible by 6.

EX3(b)

$f_{0} = 0, f_{1} = f_{2} = 1, f_{3} = 2, f_{4} = 3, \dots$ ， $f_{0}$ 能被 3 整除，且 n=0 可被 4 整除。并且 $f_{1}, f_{2}, f_{3}$ 均不能被 3 整除， $f_{4} = 3$ 可被 3 整除，且 n=4 被 4 整除。

下面使用数学归纳法证明，当 n 被 4 整除时， $f_{n}$ 一定被 3 整除。

设 $f_{4 m}$ 被 3 整除，且 $m \geq 1$ 。

\begin{aligned} f_{n} = & f_{n - 1} + f_{n - 2} \\ = & 2 f_{n - 2} + f (n - 3) \\ = & 3 f_{n - 3} + f_{n - 4} \end{aligned}

因此 $f_{n}$ 与 $f_{n - 4}$ 模三同余，即 $f_{n} \equiv f_{n - 4} (m o d 3)$ ，并且 $f_{0} = 0, f_{1} = f_{2} = 1, f_{3} = 2, f_{4} = 3$ ，因而 $f_{n}$ 被 3 整除当且仅当 n 可被 4 整除。

EX3PS

从周期性的角度入手，验证了当 $n$ 为 4 的倍数时 $f_{n}$ 可被 3 整除，并且当 $n$ 不是 4 的倍数时， $f_{n}$ 也一定不能被 3 整除。

EX4

Prove that the Fibonacci sequence is the solution of the recurrence relation
$a_{n} = 5 a_{n - 4} + 3 a_{n - 5}, (n \geq 5),$
where ao = 0, al = 1, a2 = 1, a3 = 2, and U4 = 3. Then use this formula to show that the Fibonacci numbers satisfy the condition that $f_{n}$ is divisible by 5 if and only if n is divisible by 5.

连续使用 $a_{n} = a_{n - 1} + a_{n - 2}$ 进行代换，

\begin{aligned} a_{n} = & a_{n - 1} + a_{n - 2} \\ = & 2 a_{n - 2} + a_{n - 3} \\ = & 3 a_{n - 3} + 2 a_{n - 4} \\ = & 5 a_{n - 4} + 3 a_{n - 5} \end{aligned}

因此 $a_{n}$ 与 $a_{n - 5}$ 模 5 同余，即 $a_{n} \equiv a_{n - 5} (m o d 5)$ 。并且由 $a_{0} = 0, a_{1} = 1, a_{2} = 1, a_{3} = 2, a_{4} = 3$ 可知，当且仅当 n 被 5 整除时， $f_{n} m o d 5 = 0$ 。

EX5

By examining the Fibonacci sequence, make a conjecture about when $f_{n}$ is divisible by 7 and then prove your conjecture.

对斐波那契数列 $f_{n}$ 能被 7 整除，当且仅当 n 能被 8 整除。

EX6 ⭐

* Let m and n be positive integers. Prove that if m is divisible by n, then $f_{m}$ is divisible by $f_{n}$ .

EX7 ⭐

* Let m and n be positive integers whose greatest common divisor is d. Prove that the greatest common divisor of the Fibonacci numbers $f_{m}$ and $f_{n}$ is the Fibonacci number $f_{d}$ .

EX8

Consider a 1-by-n chessboard. Suppose we color each square of the chessboard with one of the two colors red and blue. Let $h_{n}$ be the number of colorings in which no two squares that are colored red are adjacent. Find and verify a recurrence relation that hn satisfies. Then derive a formula for hn .

如果第一个方块着成红色，那么第二个方块只能着成蓝色，问题转化为 $1 \times (n - 2)$ 棋盘着色问题；如果第一个方块着成蓝色，问题转化为 $1 \times (n - 1)$ 棋盘着色问题；因此， $h_{n} = h_{n - 1} + h_{n - 2}$ 。

并且有初始项 $h_{0} = 1, h_{1} = 2$ ，显然 $h_{n} = f_{n + 2}$ 。

EX9

Let $h_{n}$ equal the number of different ways in which the squares of a 1-by-n chessboard can be colored, using the colors red, white, and blue so that no two squares that are colored red are adjacent. Find and verify a recurrence relation that $h_{n}$ satisfies. Then find a formula for $h_{n}$ .

考虑第一个方框放红色，那么第二个方块只能放白色或蓝色，问题转化为 $h_{n - 2}$ ；考虑第一个方块放白色或蓝色，那么问题转化为 $h_{n - 1}$ 。

h_{n} = 2 h_{n - 1} + 2 h_{n - 2}, h_{0} = 1, h_{1} = 3

求解方程 $x^{2} = 2 x + 2$ ，对应 $h_{n}$ 的通解为 $h_{n} = c_{1} (1 + \sqrt{3})^{n} + c_{2} (1 - \sqrt{3})^{n}$ 。

带入初始值 $h_{0} = 1, h_{1} = 3$ 可以求出常系数 $c_{1} = \frac{1}{2} + \frac{\sqrt{3}}{3}, c_{2} = \frac{1}{2} - \frac{\sqrt{3}}{3}$ 。

h_{n} = \frac{3 + 2 \sqrt{3}}{6} (1 + \sqrt{3})^{n} + \frac{3 - 2 \sqrt{3}}{6} (1 - \sqrt{3})^{n}, n = 0, 1, 2, \dots

EX10

Suppose that, in his problem, Fibonacci had placed two pairs of rabbits in the enclosure at the beginning of a year. Find the number of pairs of rabbits in the enclosure after one year. More generally, find the number of pairs of rabbits in the enclosure after n months.

设第 t 个月时有 $g_{t}$ 个兔子，满足 $g_{t} = g_{t - 1} + g_{t - 2}, g_{0} = 0, g_{1} = 2$ ，可以求出通解，

g_{t} = \frac{2}{\sqrt{5}} {(\frac{1 + \sqrt{5}}{2})}^{t} - \frac{2}{\sqrt{5}} {(\frac{1 - \sqrt{5}}{2})}^{t} = 2 f_{t}

第一个月再过 n 个月是第 n+1 月，因此有 $g_{n + 1}$ 对兔子。

提示

本题以 n 作为一个常量（n 个月后），为了区分就需要把未知量设为 t。

EX11

The Lucas numbers $l_{0}, l_{1}, l_{2}, \dots, l_{n}, \dots$ are defined using the same recurrence relation defining the Fibonacci numbers, but with different initial conditions:
$l_{n} = l_{n - 1} + l_{n - 2}, (n \geq 2), l_{0} = 2, l_{1} = 1$
Prove that
(a) $l_{n} = f_{n - 1} + f_{n + 1} for n \geq 1$
(b) $l_{0}^{2} + l_{1}^{2} + \dots + l_{n}^{2} = l_{n} l_{n + 1} + 2 for n \geq 0$

EX11(a)

设 $Z_{n} = f_{n - 1} + f_{n + 1} - l_{n}, n \geq 1$ ， $Z_{1} = f_{0} + f_{2} - l_{1} = 0 + 1 - 1 = 0$ ； $Z_{2} = f_{1} + f_{3} - l_{2} = 1 + 2 - 3 = 0$ 。

又因为 $Z_{n} = Z_{n - 1} + Z_{n - 2}, n \geq 3$ ，所以 $Z_{n} = 0, n \geq 1$ 。即有，

l_{n} = f_{n - 1} + f_{n + 1}, n \geq 1

EX11(b)

因为 $l_{n + 1} = l_{n} + l_{n - 1}$ ，所以 $l_{n}^{2} = l_{n} (l_{n + 1} - l_{n - 1}), n \geq 1$ 。

\begin{aligned} l_{0}^{2} + l_{1}^{2} + \dots + l_{n}^{2} = & l_{0}^{2} + \sum_{i = 1}^{n} l_{i}^{2} \\ = & 4 + (l_{1} l_{2} - l_{1} l_{0}) + (l_{2} l_{3} - l_{2} l_{1}) + \dots + (l_{n} l_{n + 1} - l_{n} l_{n - 1}) \\ = & 4 + l_{n} l_{n + 1} - l_{1} l_{0} \\ = & l_{n} l_{n + 1} + 2 \end{aligned}

EX12

Let $h_{0}, h_{1}, h_{2}, \dots, h_{n}, \dots$ be the sequence defined by
$h_{n} = n^{3}, (n \geq 0)$
Show that $h_{n} = h_{n - 1} + 3 n^{2} - 3 n + 1$ is the recurrence relation for the sequence.

带入 $h_{n - 1} = (n - 1)^{3}$ 化简。

EX13

Determine the generating function for each of the following sequences:
(a) $c^{0} = 1, c, c^{2}, . . ., c^{n}, . . .$
(b) $1, - 1, 1, - 1, . . ., (- 1)^{n}, . . .$
(c) $(\binom{α}{0}), - (\binom{α}{1}), (\binom{α}{2}), . . ., (- 1)^{n} (\binom{α}{n}), . . .,$ ( $α$ is a real number)
(d) $1, \frac{1}{1!}, \frac{1}{2!}, . . ., \frac{1}{n!}, . . .$
(e) $1, - \frac{1}{1!}, \frac{1}{2!}, . . ., (- 1)^{n} \frac{1}{n!}, . . .$

无穷数列 $h_{0}, h_{1}, h_{2}, \dots, h_{n} ， \dots$ 对应的生成函数为

g (x) = h_{0} + h_{1} x + h_{2} x^{2} + \dots + h_{n} x^{n} \dots

EX13(a)

\begin{aligned} g (x) = & 1 + c x + c^{2} x^{2} + \dots + c^{n} x^{n} + \dots \\ = & 1 + (c x) + (c x)^{2} + \dots + (c x)^{n} + \dots \\ = & \frac{1}{1 - c x} \end{aligned}

EX13(b)

\begin{aligned} g (x) = & 1 - x + x^{2} + \dots + (- 1)^{n} x^{n} + \dots \\ = & 1 + (- x) + (- x)^{2} + \dots + (- x)^{n} + \dots \\ = & \frac{1}{1 + x} \end{aligned}

EX13(c)

\begin{aligned} g (x) = & (\binom{α}{0}) - (\binom{α}{1}) x + (\binom{α}{2}) x^{2} + \dots + (- 1)^{n} (\binom{α}{n}) x^{n} + \dots \\ = & \sum_{k = 0}^{\infty} (\binom{α}{k}) (- x)^{k} \\ = & (1 - x)^{α} \end{aligned}

EX13(d)

\begin{aligned} g (x) = & 1 + \frac{1}{1!} x + \frac{1}{2!} x^{2} + \dots + \frac{1}{n!} x^{n} + \dots \\ = & e^{x} \end{aligned}

EX13(e)

\begin{aligned} g (x) = & 1 - \frac{1}{1!} x + \frac{1}{2!} x^{2} - \dots + (- 1)^{n} \frac{1}{n!} x^{n} + \dots \\ = & e^{- x} \end{aligned}

EX14

Let S be the multiset ${\infty \cdot e_{1}, \infty \cdot e_{2}, \infty \cdot e_{3}, \infty \cdot e_{4}}$ Determine the generating function for the sequence $h_{0}, h_{1}, h_{2}, \dots, h_{n}, \dots$ , where $h_{n}$ is the number of n-combinations of S with the following added restrictions:
(a) Each $e_{i}$ occurs an odd number of times.
(b) Each $e_{i}$ occurs a multiple-of-3 number of times.
(c) The element $e_{1}$ does not occur, and $e_{2}$ occurs at most once.
(d) The element $e_{1}$ occurs 1,3, or 11 times, and the element $e_{2}$ occurs 2,4, or 5 times.
(e) Each $e_{i}$ occurs at least 10 times.

EX14(a)

\begin{aligned} g (x) = & (x + x^{3} + x^{5} + \dots) (x + x^{3} + x^{5} + \dots) (x + x^{3} + x^{5} + \dots) (x + x^{3} + x^{5} + \dots) \\ = & {(\frac{x}{1 - x^{2}})}^{4} \end{aligned}

EX14(b)

\begin{aligned} g (x) = & (1 + x^{3} + x^{6} + \dots) (1 + x^{3} + x^{6} + \dots) (1 + x^{3} + x^{6} + \dots) (1 + x^{3} + x^{6} + \dots) \\ = & \frac{1}{(1 - x^{3})^{4}} \end{aligned}

EX14(c)

\begin{aligned} g (x) = & (1) (1 + x) (1 + x + x^{2} + x^{3} + \dots) (1 + x + x^{2} + x^{3} + \dots) \\ = & \frac{1 + x}{(1 - x)^{2}} \end{aligned}

EX14(d)

\begin{aligned} g (x) = & (x + x^{3} + x^{11}) (x^{2} + x^{4} + x^{5}) (1 + x + x^{2} + x^{3} + \dots) (1 + x + x^{2} + x^{3} + \dots) \\ = & \frac{(x + x^{3} + x^{11}) (x^{2} + x^{4} + x^{5})}{(1 - x)^{2}} \end{aligned}

EX14(e)

\begin{aligned} g (x) = & (x^{10} + x^{11} + \dots) (x^{10} + x^{11} + \dots) (x^{10} + x^{11} + \dots) (x^{10} + x^{11} + \dots) \\ = & x^{40} (1 + x^{2} + x^{3} + \dots) (1 + x^{2} + x^{3} + \dots) (1 + x^{2} + x^{3} + \dots) (1 + x^{2} + x^{3} + \dots) \\ = & \frac{x^{40}}{(1 - x)^{4}} \end{aligned}

EX15

Determine the generating function for the sequence of cubes
$0, 1, 8, \dots, n^{3}, \dots$

由第 5 章 EX20 知，

n^{3} = 6 (\binom{n}{3}) + 6 (\binom{n}{2}) + (\binom{n}{1})

\begin{aligned} g (x) = & x + 8 x^{+} \dots + n^{3} x^{2} + \dots \\ = & \sum_{n = 0}^{\infty} n^{3} x^{k} \\ = & \sum_{n = 0}^{\infty} 6 (\binom{n}{3}) x^{n} + \sum_{n = 0}^{\infty} 6 (\binom{n}{2}) x^{n} + \sum_{n = 0}^{\infty} (\binom{n}{1}) x^{n} \\ = & 6 x^{3} \sum_{n = 3}^{\infty} (\binom{n}{3}) x^{n - 3} + 6 x^{2} \sum_{n = 2}^{\infty} (\binom{n}{2}) x^{n - 2} + x \sum_{n = 1}^{\infty} (\binom{n}{1}) x^{n - 1} \\ = & 6 x^{3} \sum_{n = 0}^{\infty} (\binom{n + 3}{3}) x^{n} + 6 x^{2} \sum_{n = 0}^{\infty} (\binom{n + 2}{2}) x^{n} + x \sum_{n = 0}^{\infty} (\binom{n + 1}{1}) x^{n} \end{aligned}

由第 5 章 EX43 知，

\frac{1}{(1 - z)^{m}} = \sum_{n = 0}^{\infty} (\binom{m + n - 1}{n}) z^{n}, | z | < 1

因此，

\begin{aligned} g (x) = & 6 x^{3} \sum_{n = 0}^{\infty} (\binom{n + 3}{3}) x^{n} + 6 x^{2} \sum_{n = 0}^{\infty} (\binom{n + 2}{2}) x^{n} + x \sum_{n = 0}^{\infty} (\binom{n + 1}{1}) x^{n} \\ = & 6 x^{3} \frac{1}{(1 - x)^{4}} + 6 x^{2} \frac{1}{(1 - x)^{3}} + x \frac{1}{(1 - x)^{2}} \\ = & \frac{x (x^{2} + 4 x + 1)}{(1 - x)^{4}} \end{aligned}

EX16

Formulate a combinatorial problem for which the generating function is
$(1 + x + x^{2}) (1 + x^{2} + x^{4} + x^{6}) (1 + x^{2} + x^{4} + \dots) (x + x^{2} + x^{3} + \dots)$

果篮中苹果、香蕉、西瓜和桃子，求苹果不超过 2 个，香蕉为不超过 6 个且为偶数，西瓜是偶数个，桃子至少有 1 个的组合数。

EX17

Determine the generating function for the number hn of bags of fruit of apples, oranges, bananas, and pears in which there are an even number of apples, at most two oranges, a multiple of three number of bananas, and at most one pear. Then find a formula for hn from the generating function.

\begin{aligned} g (x) = & (1 + x^{2} + x^{4} + \dots) (1 + x + x^{2}) (1 + x^{3} + x^{6} + \dots) (1 + x) \\ = & \frac{1}{(1 - x)^{2}} \\ = & \sum_{n = 0}^{\infty} (n + 1) x^{n} \end{aligned}

因此 $h_{n} = (n + 1)$ 。

翻译错误

注意黑皮书题干中的翻译错误，英文原意是至多有两个橙子。

不管怎么描述，本题都是可解的。在做题时需要认真读清题目。

EX18

Determine the generating function for the number $h_{n}$ of nonnegative integral solutions of
$2 e_{1} + 5 e_{2} + e_{3} + 7 e_{4} = n$

令 $f_{1} = 2 e_{1}, f_{2} = 5 e_{2}, f_{3} = e_{3}, f_{4} = 7 e_{4}$ ，所以有 $f_{1} + f_{2} + f_{3} + f_{4} = n$ ，其中 $f_{1}$ 是 2 的倍数， $f_{2}$ 是 5 的倍数， $f_{3}$ 是 1 的倍数， $f_{4}$ 是 7 的倍数。有生成函数，

\begin{aligned} g (x) = & (1 + x^{2} + x^{4} + \dots) (1 + x^{5} + x^{10} + \dots) (1 + x + x^{2} + x^{3} + \dots) (1 + x^{7} + x^{14} + \dots) \\ = & \frac{1}{1 - x^{2}} \frac{1}{1 - x^{5}} \frac{1}{1 - x} \frac{1}{1 - x^{7}} \end{aligned}

EX19

Let $h_{0}, h_{1}, h_{2}, . . ., h_{n}, . . .$ be the sequence defined by $h_{n} = (\binom{n}{2}), (n \geq 0)$ . Determine the generating function for the sequence.

\begin{aligned} g (x) = & \sum_{n = 0}^{\infty} h_{n} x^{n} \\ = & \sum_{n = 0}^{\infty} (\binom{n}{2}) x^{n} \\ = & x^{2} \sum_{n = 2}^{\infty} (\binom{n}{2}) x^{n - 2} \\ = & x^{2} \sum_{n = 0}^{\infty} (\binom{n + 2}{2}) x^{n} \\ = & \frac{x^{2}}{(1 - x)^{3}} \end{aligned}

简评

本题可以算是 EX15 的一个子问题

EX20

Let $h_{0}, h_{1}, h_{2}, . . ., h_{n}, . . .$ be the sequence defined by $h_{n} = (\binom{n}{3}), (n \geq 0)$ . Determine the generating function for the sequence.

\begin{aligned} g (x) = & \sum_{n = 0}^{\infty} h_{n} x^{n} \\ = & \sum_{n = 0}^{\infty} (\binom{n}{3}) x^{n} \\ = & x^{3} \sum_{n = 3}^{\infty} (\binom{n}{3}) x^{n - 3} \\ = & x^{3} \sum_{n = 0}^{\infty} (\binom{n + 3}{3}) x^{n} \\ = & \frac{x^{3}}{(1 - x)^{4}} \end{aligned}

EX21 ⭐

* Let $h_{n}$ denote the number of regions into which a convex polygonal region with n + 2 sides is divided by its diagonals, assuming no three diagonals have a common point. Define $h_{0}$ = 0. Show that
$h_{n} = h_{n - 1} + (\binom{n + 1}{3}) + n, (n \geq 1)$
Then determine the generating function and obtain a formula for $h_{n}$ .

EX22

Determine the exponential generating function for the sequence of factorials: $0!, 1!, 2!, 3!, . . ., n!, \dots$ .

\begin{aligned} g^{(e)} (x) = & \sum_{n = 0}^{\infty} h_{n} \frac{x^{n}}{n!} \\ = & \sum_{n = 0}^{\infty} n! \frac{x^{n}}{n!} \\ = & \sum_{n = 0}^{\infty} x^{n} \\ = & \frac{1}{1 - x} \end{aligned}

EX23

Let $α$ be a real number. Let the sequence $h_{0}, h_{1}, h_{2}, . . ., h_{n}, . . .$ be defined by $h_{0} = 1$ , and $h_{n} = α (α - 1) \dots (α - n + 1), (n \geq 1)$ . Determine the exponential generating function for the sequence.

\begin{aligned} g^{(e)} (x) = & \sum_{n = 0}^{\infty} h_{n} \frac{x^{n}}{n!} \\ = & \sum_{n = 0}^{\infty} α (α - 1) \dots (α - n + 1) \frac{x^{n}}{n!} \\ = & \sum_{n = 0}^{\infty} (\binom{α}{n}) x^{n} \\ = & (1 + x)^{α} \end{aligned}

EX24

Let S be the multiset ${\infty \cdot e_{1}, \infty \cdot e_{2}, \infty \cdot e_{3}, \dots, \infty \cdot e_{k}}$ Determine the exponential generating function for the sequence $h_{0}, h_{1}, h_{2}, \dots, h_{n}, \dots$ , where $h_{0} = 1$ and, for $n \geq 1$ ,
(a) $h_{n}$ equals the number of n-permutations of S in which each object occurs an odd number of times.
(b) $h_{n}$ equals the number of n-permutations of S in which each object occurs at least four times.
(c) $h_{n}$ equals the number of n-permutations of S in which $e_{1}$ occurs at least once, $e_{2}$ occurs at least twice, ... , $e_{k}$ occurs at least $k$ times.
(d) $h_{n}$ equals the number of n-permutations of S in which $e_{1}$ occurs at most once, $e_{2}$ occurs at most twice, ... , $e_{k}$ occurs at most $k$ times.

EX24(a)

\begin{aligned} g^{(e)} (x) = & (\frac{x}{1!} + \frac{x^{3}}{3!} + \frac{x^{5}}{5!} + \dots) (\frac{x}{1!} + \frac{x^{3}}{3!} + \frac{x^{5}}{5!} + \dots) \dots (\frac{x}{1!} + \frac{x^{3}}{3!} + \frac{x^{5}}{5!} + \dots) \\ = & (\frac{x}{1!} + \frac{x^{3}}{3!} + \frac{x^{5}}{5!} + \dots)^{k} \\ = & {(\frac{e^{x} - e^{- x}}{2})}^{k} \end{aligned}

EX24(b)

\begin{aligned} G^{(e)} (x) = & \frac{x^{4}}{4!} + \frac{x^{5}}{5!} + \frac{x^{6}}{6!} + \dots \\ = & e^{x} - 1 - x - \frac{x^{2}}{2!} - \frac{x^{3}}{3!} \end{aligned}

并且指数生成函数为 $g^{(e)} (x) = (G^{(e)} (x))^{k}$ 。

EX24(c)

\begin{aligned} G_{k}^{(e)} (x) = & \frac{x^{k}}{k!} + \frac{x^{k + 1}}{(k + 1)!} + \frac{x^{k + 2}}{(k + 2)!} + \dots \\ = & e^{x} - \sum_{j = 0}^{k - 1} \frac{x^{j}}{j!} \end{aligned}

指数生成函数为 $g^{(e)} (x) = G_{1}^{(e)} (x) G_{2}^{(e)} (x) \dots G_{k}^{(e)} (x)$ 。

EX24(d)

\begin{aligned} G_{k}^{(e)} (x) = & 1 + \frac{x}{1!} + \frac{x^{2}}{2!} + \dots + \frac{x^{k}}{k!} \\ = & \sum_{j = 0}^{k} \frac{x^{j}}{j!} \end{aligned}

指数生成函数为 $g^{(e)} (x) = G_{1}^{(e)} (x) G_{2}^{(e)} (x) \dots G_{k}^{(e)} (x)$ 。

EX25

Let $h_{n}$ denote the number of ways to color the squares of a 1-by-n board with the colors red, white, blue, and green in such a way that the number of squares colored red is even and the number of squares colored white is odd. Determine the exponential generating function for the sequence $h_{0}, h_{1}, h_{2}, \dots, h_{n}, \dots$ , and then find a simple formula for $h_{n}$ .

\begin{aligned} g^{(e)} (x) = & (1 + \frac{x^{2}}{2!} + \frac{x^{4}}{4!} + \dots) (\frac{x}{1!} + \frac{x^{3}}{3!} + \frac{x^{5}}{5!} + \dots) (1 + \frac{x}{1!} + \frac{x^{2}}{2!} + \dots) (1 + \frac{x}{1!} + \frac{x^{2}}{2!} + \dots) \\ = & \frac{e^{x} + e^{- x}}{2} \frac{e^{x} - e^{- x}}{2} e^{x} e^{x} \\ = & e^{2 x} \frac{e^{2 x} - e^{- 2 x}}{4} \\ = & \frac{e^{4 x} - 1}{4} \\ = & \frac{1}{4} (4 x + \frac{(4 x)^{2}}{2!} + \dots) \\ = & \sum_{n = 1}^{\infty} 4^{n - 1} \frac{x^{n}}{n!} \end{aligned}

因此 $h_{n} = 4^{n - 1}, (n \geq 1)$ ，当 n=0 时， $h_{0} = 1$ 。

EX26

Determine the number of ways to color the squares of a 1-by-n chessboard, using the colors red, blue, green, and orange if an even number of squares is to be colored red and an even number is to be colored green.

\begin{aligned} g^{(e)} (x) = & (1 + \frac{x^{2}}{2!} + \frac{x^{4}}{4!} + \dots) (1 + \frac{x^{2}}{2!} + \frac{x^{4}}{4!} + \dots) (1 + \frac{x}{1!} + \frac{x^{2}}{2!} + \dots) (1 + \frac{x}{1!} + \frac{x^{2}}{2!} + \dots) \\ = & \frac{e^{x} + e^{- x}}{2} \frac{e^{x} + e^{- x}}{2} e^{x} e^{x} \\ = & e^{2 x} \frac{e^{2 x} + e^{- 2 x} + 2}{4} \\ = & \frac{e^{4 x} + 2 e^{2 x} + 1}{4} \\ = & \frac{1}{4} (1 + (4 + 2 \times 2) x + \frac{(4^{2} + 2 \times 2^{2}) x^{2}}{2!} + \dots) \\ = & \frac{1}{4} + \sum_{n = 1}^{\infty} (4^{n - 1} + 2^{n - 1}) \frac{x^{n}}{n!} \end{aligned}

因此 $h_{n} = 4^{n - 1} + 2^{n - 1}, (n \geq 1)$ ，当 n=0 时， $h_{0} = 1$ 。

EX27

Determine the number of n-digit numbers with all digits odd, such that 1 and 3 each occur a nonzero, even number of times.

问题等价于 ${\infty \cdot 1, \infty \cdot 3, \infty \cdot 5, \infty \cdot 7, \infty \cdot 9}$ 的多重集合 n 排列数，

G_{1}^{(e)} (x) = G_{3}^{(e)} (x) = \frac{x^{2}}{2!} + \frac{x^{4}}{4!} + \dots = \frac{e^{x} + e^{- x}}{2} - 1

G_{5}^{(e)} (x) = G_{7}^{(e)} (x) = G_{9}^{(e)} (x) = e^{x}

指数生成函数为，

\begin{aligned} g^{(e)} (x) = & G_{1}^{e} (x) G_{3}^{e} (x) \dots G_{9}^{e} (x) \\ = & {(\frac{e^{x} + e^{- x} - 2}{2})}^{2} e^{3 x} \\ = & \frac{e^{5 x} - 4 e^{4 x} + 6 e^{3 x} - 4 e^{2 x} + e^{x}}{4} \end{aligned}

因此 $h_{n} = \frac{5^{n} - 4 \times 4^{n} + 6 \times 3^{n} - 4 \times 2^{n} + 1}{4}$ 。

EX28

Determine the number of n-digit numbers with all digits at least 4, such that 4 and 6 each occur an even number of times, and 5 and 7 each occur at least once, there being no restriction on the digits 8 and 9.

问题等价于 ${\infty \cdot 4, \infty \cdot 5, \infty \cdot 6, \infty \cdot 7, \infty \cdot 8, \infty \cdot 9}$ 的多重集合 n 排列数。

G_{4}^{(e)} (x) = G_{6}^{(e)} (x) = 1 + \frac{x^{2}}{2!} + \frac{x^{4}}{4!} + \dots = \frac{e^{x} + e^{- x}}{2}

G_{5}^{(e)} (x) = G_{7}^{(e)} (x) = e^{x} - 1

指数生成函数为，

\begin{aligned} g^{(e)} (x) = & G_{4}^{e} (x) G_{5}^{e} (x) \dots G_{9}^{e} (x) \\ = & {(\frac{e^{x} + e^{- x}}{2})}^{2} {(e^{x} - 1)}^{2} e^{2 x} \\ = & \frac{e^{6 x} - 2 e^{5 x} + 3 e^{4 x} - 4 e^{3 x} + 3 e^{2 x} - 2 e^{x} + 1}{4} \end{aligned}

因此 $h_{n} = \frac{6^{n} - 2 \times 5^{n} + 3 \times 4^{n} - 4 \times 3^{n} + 3 \times 2^{n} - 2}{4}, (n \geq 0)$ ， $h_{0} = 0$ 。

强调

需要根据题目的意义来决定初始项 $h_{0}$ ，本题 $h_{0}$ 是 0 位数中满足性质的个数，而 0 位数不可能满足5 和 7 至少出现一次。

EX29

We have used exponential generating functions to show that the number hn of n-digit numbers with each digit odd, where the digits 1 and 3 occur an even number of times, satisfies the formula
$h_{n} = \frac{5^{n} + 2 \times 3^{n} + 1}{4}, (n \geq 0)$
Obtain an laternative derivation of this formula.

根据 n 位数中 1 和 3 出现数量的奇偶性可以分类，

种类	1 的数量	3 的数量
$a_{n}$	奇数	奇数
$b_{n}$	奇数	偶数
$c_{n}$	偶数	奇数
$h_{n}$	偶数	偶数

对于 $a_{n}$ 考虑移除最低位的数字，可以划分为三种情况：移除的数字为 1，问题变为 $c_{n - 1}$ ；移除的数字为 3，问题变为 $b_{n - 1}$ ，移除的数字是 5、7 或 9，问题变为 $3 a_{n - 1}$ 。即有 $a_{n} = c_{n - 1} + b_{n - 1} + 3 a_{n - 1}$ 。此外所有的可能总数是 $5^{n}$ 。可以得到方程组，

{\begin{cases} a_{n} = c_{n - 1} + b_{n - 1} + 3 a_{n - 1} \\ b_{n} = h_{n - 1} + a_{n - 1} + 3 b_{n - 1} \\ c_{n} = a_{n - 1} + h_{n - 1} + 3 c_{n - 1} \\ h_{n} = b_{n - 1} + c_{n - 1} + 3 h_{n - 1} \\ a_{n} + b_{n} + c_{n} + h_{n} = 5^{n} \end{cases}

初始条件， $a_{0} = b_{0} = c_{0} = 0, h_{0} = 1$ 。由对称性知 $b_{n} = c_{n}$ ，可得 $a_{n} + 2 b_{n} + h_{n} = 5^{n}, h_{n} - 3 h_{n - 1} = 2 b_{n - 1}$ ，用后式消去前式中的 $b_{n}$ 得 $a_{n} + h_{n + 1} - 2 h_{n} = 5^{n}$ 。

写出该式子的下一项 $a_{n - 1} + h_{n} - 2 h_{n - 1} = 5^{n}$ ，递推一项做差并且调整 $h_{n}$ 为最高次，进而得到 $h_{n} - 4 h_{n - 1} + 3 h_{n - 2} = 2 \times 5^{n - 2}$ 。

解方程略，可得其次递推关系的解 $H_{n} = c_{1} 3^{n} + c_{2}$ ，非齐次递推关系的特解为 $H_{n}^{*} = \frac{x^{n}}{4}$ 。

所以通解为 $h_{n} = c_{1} 3^{n} + c_{2} + \frac{5^{n}}{4}$ 。

对于 1 位数， $h_{1} = 3$ 。带入 $h_{0} = 1, h_{1} = 3$ ，解得 $c_{1} = \frac{1}{2}, c_{2} = \frac{1}{4}$ 。进而求出，

h_{n} = \frac{5^{n} + 2 \times 3^{n} + 1}{4}

EX30

We have used exponential generating functions to show that the number hn of ways to color the squares of a 1-by-n board with the colors red, white, and blue, where the number of red squares is even and there is at least one blue square, satisfies the formula
$h_{n} = \frac{3^{n} - 2^{n} + 1}{2}, (n \geq 1)$
with $h_{0} = 0$ . Obtain an alternative derivation of this formula by finding a recurrence relation satisfied by $h_{n}$ and then solving the recurrence relation.

种类	红色	蓝色
$a_{n}$	奇数	无限制
$b_{n}$	偶数	$= 0$
$h_{n}$	偶数	$\geq 1$

以 $a_{n}$ 为例，考虑删除第一格。如果第一格为蓝色或白色，问题变为 $2 a_{n - 1}$ ；如果第一格为红色，问题转化为从剩余 n-1 格中选出偶数个红格，总染色方案数为 $3^{n - 1}$ ，其中红色为奇数的方案是 $a^{n - 1}$ ，所以有 $3^{n - 1} - a_{n - 1}$ 种方案选出偶数个红格。所以有 $a_{n} = 2 a_{n - 1} + 3^{n - 1} - a_{n - 1} = a_{n - 1} + 3^{n - 1}$ 。

对于 $b_{n}$ ，如果第一格为白色，问题转化为 $b_{n - 1}$ ，如果第一格为红色，同上有 $2^{n - 1} - b_{n - 1}$ ，因此得 $b_{n} = 2^{n - 1}$ 。

$a_{n} + b_{n} + h_{n}$ 为总方案数 $3^{n}$ ，可以递推做差得 $h_{n} - h_{n - 1} = 3^{n - 1} - 2^{n - 1}$ 。解方程过程略。

初始值 $h_{0} = 1$ 。

提示

利用好奇偶两种对立状态。
题目强调要写出 $h_{n}$ 的递推式，实际上容易先求出 $a_{n}$ ，然后带入 $a_{n} + b_{n} + h_{n} = 3^{n}$ 求出 $h_{n}$ ，但这样不满足题目要求的解法。

EX31

Solve the recurrence relation $h_{n} = 4 h_{n - 2}, (n \geq 2)$ with initial values $h_{0} = 0$ and $h_{1} = 1$ .

h_{n} = c_{1} 2^{n} + c_{2} (- 2)^{n}

带入初始值解得， $h_{n} = \frac{2^{n} - (- 2)^{n}}{4}, (n \geq 0)$ 。

EX32

Solve the recurrence relation $h_{n} = (n + 2) h_{n - 1}, (n \geq 1)$ with initial value $h_{0} = 2$ .

\begin{aligned} h_{n} = & \frac{h_{n}}{h_{n - 1}} \frac{h_{n - 1}}{h_{n - 2}} \dots \frac{h_{1}}{h_{0}} h_{0} \\ = & (n + 2) \times (n + 1) \times \dots \times (1 + 2) \times 2 \\ = & (n + 2)! n \geq 0 \end{aligned}

EX33

Solve the recurrence relation $h_{n} = h_{n - 1} + 9 h_{n - 2} - 9 h_{n - 3}, (n \geq 3)$ with initial values $h_{0} = 0, h_{1} = 1$ , and $h_{2} = 2$ .

方程 $x^{3} = x^{2} + 9 x - 9 = 0$ 的解为 $x_{1} = 3, x_{3} = - 3, x_{3} = 1$ 。

$h_{n} = c_{1} 3^{n} + c_{2} (- 3)^{n} + c_{3}$ ，带入初始值有 $h_{n} = 3^{n - 1} + \frac{(- 3)^{n - 1}}{4} - \frac{1}{4}, (n \geq 0)$ 。

EX34

Solve the recurrence relation $h_{n} = 8 h_{n - 1} - 16 h_{n - 2}, (n \geq 2)$ with initial values $h_{0} = - 1$ and $h_{1} = 0$ .

$h_{n} = c_{1} 4^{n} + c_{2} n \cdot 4^{n}$ ，带入初始值有 $h_{n} = (n - 1) 4^{n}, (n \geq 0)$ 。

EX35

Solve the recurrence relation $h_{n} = 3 h_{n - 2} - 2 h_{n - 3}, (n \geq 3)$ with initial values $h_{0} = 1, h_{1} = 0$ , and $h_{2} = 0$ .

$h_{n} = (c_{1} + c_{2} n) + c_{3} (- 2)^{n}$ ，带入初始值有 $h_{n} = (\frac{8}{9} - \frac{2 n}{3}) + \frac{(- 2)^{n}}{9}, (n \geq 0)$ 。

EX36

Solve the recurrence relation $h_{n} = 5 h_{n - 1} - 6 h_{n - 2} - 4 h_{n - 3} + 8 h_{n - 4}, (n \geq 4)$ with initial values $h_{0} = 0, h_{1} = 1, h_{2} = 1$ , and $h_{3} = 2$ .

方程 $x^{4} = 5 x^{3} - 6 x^{2} - 4 x + 8$ 的解为 $x_{1} = x_{2} = x_{3} = 2, x_{4} = - 1$ 。

$h_{n} = (c_{1} n^{2} + c_{2} n + c_{3}) 2^{n} + c_{4} (- 1)^{n}$ ，带入初始值有 $h_{n} = (- \frac{n^{2}}{24} + \frac{7 n}{72} + \frac{8}{27}) 2^{n} - \frac{8 \cdot (- 1)^{n}}{27}, (n \geq 0)$ 。

简评

分解方程和求解四元一次方程组的计算量很大。

EX37

Determine a recurrence relation for the number an of ternary strings (made up of 0s, 1s, and 2s) of length n that do not contain two consecutive 0s or two consecutive 1s. Then find a formula for $a_{n}$ .

对长度为 n 且符合题目要求的字符串 $T_{n}$ 进行切片，按照前两个字符是否相同进行分类；如果前两个字符相同，那么只能切出 22 和 $T_{n - 2}$ ，如果前两个字符不同，每一个字符（0、1 或 2）都有两种符合题意的 $T_{n - 1}$ 。

因此得到递推公式： $a_{n} = a_{n - 2} + 2 a_{n - 1}, (n \geq 2)$ ，容易知道初始值 $a_{0} = 1, a_{1} = 3$ 。

因此求出 $a_{n} = \frac{(1 + \sqrt{2})^{n + 1}}{2} + \frac{(1 - \sqrt{2})^{n + 1}}{2}, (n \geq 0)$ 。

联想 💡

对比 EX37、EX40 和 EX9

EX38 👻

Solve the following recurrence relations by examining the first few values for a formula and then proving your conjectured formula by induction.
(a) $h_{n} = 3 h_{n - 1}, (n \geq 1); h_{0} = 1$
(b) $h_{n} = h_{n - 1} - n + 3, (n \geq 1); h_{0} = 2$
(c) $h_{n} = - h_{n - 1} + 1, (n \geq 1); h_{0} = 0$
(d) $h_{n} = - h_{n - 1} + 2, (n \geq 1); h_{0} = 1$
(e) $h_{n} = 2 h_{n - 1} + 1, (n \geq 1); h_{0} = 1$

以 EX38(b) 为例，先求出通项，再用数学归纳法验证，其余同理。

EX38(b)

先求其次递推关系的解， $H_{n} = c_{1} (1)^{n}$ ，后面的非齐次部分是一次多项式，同时隐含也是以 1 为底的指数。因此设 $H_{n}^{*} = (A n + B) n$ 。

带入递推关系求出 $A = - \frac{1}{2}, B = \frac{5}{2}$ ，带入初始量得 $h_{n} = \frac{4 + 5 n - n^{2}}{2}$ 。

数学归纳法证明过程略。

EX39

Let $h_{n}$ denote the number of ways to perfectly cover a 1-by-n board with monominoes and dominoes in such a way that no two dominoes are consecutive. Find, but do not solve, a recurrence relation and initial conditions satisfied by $h_{n}$ .

容易验证初始值 $h_{0} = h_{1} = 1, h_{2} = 2$ ，当 $n \geq 3$ 时，如果第一块为单牌，问题变为 $h_{n - 1}$ ，如果第一块为多米诺骨牌（ $1 \times 2$ 牌），那么临界的块只能是单牌，问题转化为 $h_{n - 3}$ 。

综上有，

h_{n} = h_{n - 1} + h_{n - 3}

简评

头一次看到专门强调只推出关系不求解的题目。

EX40

Let $a_{n}$ equal the number of ternary strings of length n made up of Os, ls, and 2s, such that the substrings 00, 01, 10, and 11 never occur. Prove that
$a_{n} = a_{n - 1} + 2 a_{n - 2}, (n \geq 2),$
with $a_{0} = 1$ and $a_{1} = 3$ . Then find a formula for $a_{n}$ .

按照第一字符是否为 2 进行划分，由题意，长度为 n 的串第一个字符是 2，问题变为 $a_{n - 1}$ ；如果第一个字符不是 2，那么只能是 0 或 1，如果为 0，则第二个字符只能是 2（因为不存在 00 和 01），同理第一格字符如果为 1，则第二个字符只能为 2，因此问题转化为 $2 a_{n - 2}$ 。综上有，

a_{n} = a_{n - 1} + 2 a_{n - 2}

长度为 0 的串，长度为 1 的串显然都不含有 00、01、10 和 11， $a_{0} = 1, a_{1} = 3$ 。

EX41

* Let 2n equally spaced points be chosen on a circle. Let $h_{n}$ denote the number of ways to join these points in pairs so that the resulting line segments do not intersect. Establish a recurrence relation for $h_{n}$ .

EX41

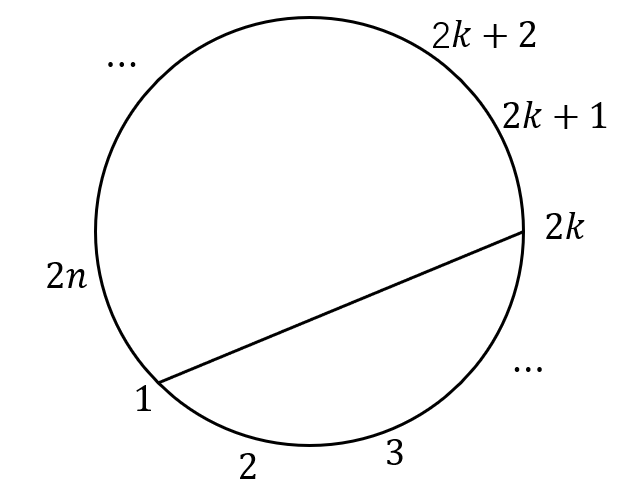
选择一端固定在 1 上的线段为基线，另一端指向 2k，圆上的 2n 个点被分为两组，一组有 2k-2 个，另一组有 2n-2k 个，同时问题 $h_{n}$ 被划分为 $h_{k - 1}$ 和 $h_{n - k}$ 。所以有，

h_{n} = \sum_{k = 1} h_{k - 1} h_{n - k}, n \geq 1, h_{0} = h_{1} = 1

显然 $h_{n}$ 与卡特兰数 $C_{n}$ 有相同的递推关系和初始项，因此，

h_{n} = \frac{1}{n + 1} (\binom{2 n}{n})

EX42 👻

Solve the monhomogeneous recurrence realtion
$\begin{aligned} h_{n} = 4 h_{n - 1} + 4^{n}, (n \geq 1) \\ h_{0} = 3 \end{aligned}$

其次递推关系的解为 $H_{n} = c_{1} 4^{n}$ ，因此设特解为 $H_{n}^{*} = A n 4^{n}$ ，求出 $A = 1$ ，带入初始项求出，

h_{n} = (n + 3) 4^{n}, n \geq 0

简评

虽然参考答案秀了技巧，把非齐次方程转化为 $h_{n} - 8 h_{n - 1} + 16 h_{n - 2} = 0$ 。但着实没有必要，按照非齐次的模板解题速度一样很快。

EX43 👻

Solve the monhomogeneous recurrence realtion
$\begin{aligned} h_{n} = 4 h_{n - 1} + 3 \times 2^{n}, (n \geq 1) \\ h_{0} = 1 \end{aligned}$

略。

EX44 👻

Solve the monhomogeneous recurrence realtion
$\begin{aligned} h_{n} = 3 h_{n - 1} - 2, (n \geq 1) \\ h_{0} = 1 \end{aligned}$

略

EX45 👻

Solve the monhomogeneous recurrence realtion
$\begin{aligned} h_{n} = 2 h_{n - 1} + n, (n \geq 1) \\ h_{0} = 1 \end{aligned}$

略

EX46 👻

Solve the monhomogeneous recurrence realtion
$\begin{aligned} h_{n} = 6 h_{n - 1} - 9 h_{n - 2} + 2 n, (n \geq 2) \\ h_{0} = 1 \\ h_{1} = 0 \end{aligned}$

略

EX47 👻

Solve the monhomogeneous recurrence realtion
$\begin{aligned} h_{n} = 4 h_{n - 1} - 4 h_{n - 2} + 3 n + 1, (n \geq 2) \\ h_{0} = 1 \\ h_{1} = 2 \end{aligned}$

略

EX48 👻

Solve the following recurrence relations by using the method of generating functions as described in Section 7.4:
(a) $h_{n} = 4 h_{n - 2}, (n \geq 2); h_{0} = 0, h_{1} = 1$
(b) $h_{n} = h_{n - 1} + h_{n - 2}, (n \geq 2); h_{0} = 1, h_{1} = 3$
(c) $h_{n} = h_{n - 1} + 9 h_{n - 2} - 9 h_{n - 3}, (n \geq 3); h_{0} = 0, h_{1} = 1, h_{2} = 2$
(d) $h_{n} = 8 h_{n - 1} - 16 h_{n - 2}, (n \geq 2); h_{0} = - 1, h_{1} = 0$
(e) $h_{n} = 3 h_{n - 2} - 2 h_{n - 3}, (n \geq 3); h_{0} = 1, h_{1} = 0, h_{2} = 0$
(f) $h_{n} = 5 h_{n - 1} - 6 h_{n - 2} - 4 h_{n - 3} + 8 h_{n - 4}, (n \geq 4); h_{0} = 0, h_{1} = 1, h_{2} = 1, h_{3} = 2$

以 EX48(b) 和 EX48(f) 为例，其余题目略。

EX48(b)

设生成函数为 $g (x) = h_{0} + h_{1} x + h_{2} x^{2} + \dots$ ，分别用 $- x$ 和 $- x^{2}$ 乘以 g(x) 得到，

\begin{aligned} - x g (x) = - h_{0} x - h_{1} x^{2} - h_{2} x^{3} - \dots \\ - x^{2} g (x) = - h_{0} x^{2} - h_{1} x^{3} - h_{2} x^{4} - \dots \end{aligned}

两边求和化简得，

(1 - x - x^{2}) g (x) = h_{0} + (h_{0} - h_{1}) x + (h_{2} - h_{1} - h_{0}) x^{2} + \dots + (h_{n} - h_{n - 1} - h_{n - 2}) x^{n} + \dots

再由 $h_{n} - h_{n - 1} - h_{n - 2} = 0, (n \geq 2)$ 知，

\begin{aligned} g (x) = & \frac{1 + 2 x}{1 - x - x^{2}} \\ = & \frac{r}{1 - r x} + \frac{s}{1 - s x} \\ = & \frac{(r + s) - 2 r s x}{1 - (r + s) x + r s x^{2}} = & \sum_{n = 0}^{\infty} (r^{n + 1} + s^{n + 1}) x^{n} \end{aligned}

其中， $r = \frac{1 + \sqrt{5}}{2}, s = \frac{1 - \sqrt{5}}{2}, r + s = 1, r s = - 1$ 。

因此， $h_{n} = r^{n + 1} + s^{n + 1}, (n \geq 0)$

EX48(f)

设生成函数为 $g (x) = h_{0} + h_{1} x + h_{2} x^{2} + \dots$ ，分别用 $- 5 x$ 、 $6 x^{2}$ 、 $4 x^{3}$ 和 $- 8 x^{4}$ 乘以 g(x) 化简得到，

\begin{aligned} g (x) = & \frac{x - 4 x^{2} + 3 x^{3}}{1 - 5 x + 6 x^{2} + 4 x^{3} - 8 x^{4}} \\ = & \frac{x - 4 x^{2} + 3 x^{3}}{(1 - 2 x)^{3} (1 + x)} \\ = & \frac{a x^{2} + b x + c}{(1 - 2 x)^{3}} + \frac{d}{1 + x} \\ = & \frac{(a - 8 d) x^{3} + (a + b + 12 d) x^{2} + (b + c - 6 d) x + (c + d)}{(1 - 2 x)^{3} (1 + x)} \end{aligned}

因此可以得到方程组，

{\begin{cases} a - 8 d = 3 \\ a + b + 12 d = - 4 \\ b + c - 6 d = 1 \\ c + d = 0 \end{cases}

解得， $a = \frac{17}{27}, b = - \frac{29}{27}, c = - \frac{8}{27}, d = \frac{8}{27}$ 。

g (x) = \frac{1}{27} \frac{17 x^{2} - 29 x - 8}{(1 - 2 x)^{3}} + \frac{8}{(1 + x)}

提示

从上面的过程可以看出使用生成函数求解的计算量极大，因此如果题目不是强调使用该方法，不要考虑使用它。

EX49

(q-binomial theorem) Prove that
$(x + y) (x + q y) (x + q^{2} y) \dots (x + q^{n - 1} y) = \sum_{k = 0}^{n} {(\binom{n}{k})}_{q} x^{n - k} y^{k},$
where
$n!_{q} = \frac{Π_{j = 1}^{n} (1 - q^{j})}{(1 - q)^{n}}$
is the q-factorial (cf. Theorem 7.2.1 replacing q in (7.14) with x) and
${(\binom{n}{k})}_{q} = \frac{n!_{q}}{k!_{q} (n - k)!_{q}}$
is the q-binomial coefficient.

采用数学归纳法证明，当 n=1 时，左边等于 $(x + y)$ ，右边等于 $\sum_{k = 0}^{1} {(\binom{1}{k})}_{q} x^{1 - k} y^{k} = {(\binom{1}{0})}_{q} x + {(\binom{1}{1})}_{q} y = x + y$ ，左右两边相等，成立。

假设取 n 时等式成立，那么取 n+1 时，左右两边同时乘 $(x + q^{n} y)$ 有，

\begin{aligned} \sum_{k = 0}^{n} {(\binom{n}{k})}_{q} x^{n - k} y^{k} (x + q^{n} y) = & \sum_{k = 0}^{n} {(\binom{n}{k})}_{q} x^{n + 1 - k} y^{k} + q^{n} \sum_{k = 0}^{n} {(\binom{n}{k})}_{q} x^{n - k} y^{k + 1} \\ = & \sum_{k = 0}^{n} {(\binom{n}{k})}_{q} x^{n + 1 - k} y^{k} + q^{n} \sum_{k = 1}^{n + 1} {(\binom{n}{k - 1})}_{q} x^{n + 1 - k} y^{k} \\ = & {(\binom{n}{0})}_{q} x^{n + 1} + \sum_{k = 1}^{n} ({(\binom{n}{k})}_{q} + q^{n} {(\binom{n}{k - 1})}_{q}) x^{n + 1 - k} y^{k} + {(\binom{n}{n})}_{q} y^{n + 1} \\ = & {(\binom{n + 1}{0})}_{q} x^{n + 1} + \sum_{k = 1}^{n} ({(\binom{n}{k})}_{q} + q^{n} {(\binom{n}{k - 1})}_{q}) x^{n + 1 - k} y^{k} + {(\binom{n + 1}{n + 1})}_{q} y^{n + 1} \\ = & \sum_{k = 0}^{n + 1} {(\binom{n + 1}{k})}_{q} x^{n + 1 - k} y^{k} \end{aligned}

即取 n+1 时等式仍成立，综上，证毕。

EX49PS

下面验证，

{(\binom{n + 1}{k})}_{q} = {(\binom{n}{k})}_{q} + q^{n} {(\binom{n}{k - 1})}_{q}

EX49 参考

q-binomial coefficients

EX50

Call a subset S of the integers {1, 2, ... ,n} extmordinary provided its smallest integer equals its size:
$min {x : x \in S} = | S |$
For example, S = {3,7,8}, is extraordinary. Let $g_{n}$ be the number of extraordinary subsets of {1, 2, ..., n}. Prove that
$g_{n} = g_{n - 1} + g_{n - 2} (n \geq 3),$
with $g_{1} = 1$ and $g_{2} = 1$ .

如果子集 S 是非凡的 k 子集，那么 S 中的最小元素是 k，其余 k-1 个元素均比 k 大，因此非凡 k 子集的个数为 $(\binom{n - k}{k - 1})$ 个，那么集合{1, 2, 3, ..., n}的所有非凡集为，

\begin{aligned} g_{n} = & \sum_{k = 1}^{n} (\binom{n - k}{k - 1}) \\ = & \sum_{k = 1}^{n} (\binom{n - k - 1}{k - 1}) + \sum_{k = 1}^{n} (\binom{n - k - 1}{k - 2}) \\ = & \sum_{k = 1}^{n} (\binom{(n - 1) - k}{k - 1}) + \sum_{k = 1}^{n} (\binom{(n - 2) - k - 1}{(k - 1) - 1}) \\ = & \sum_{k = 1}^{n} (\binom{(n - 1) - k}{k - 1}) + \sum_{h = 1}^{n} (\binom{(n - 2) - h}{h - 1}) \\ = & \sum_{k = 1}^{n - 1} (\binom{(n - 1) - k}{k - 1}) + \sum_{h = 1}^{n - 2} (\binom{(n - 2) - h}{h - 1}) \\ = & g_{n - 1} + g_{n - 2} \end{aligned}

由题意容易求出{1}的非凡集为{1}，{1, 2}的非凡集为{1}，因此 $g_{1} = g_{2} = 1$ 。

EX51

Solve the recurrence relation
$\begin{aligned} h_{n} = 3 h_{n - 1} - 4 n, (n \geq 1) & h_{0} = 2 \end{aligned}$
from Section 7.6 using generating functions.

要求使用生成函数求解非齐次递推关系。生成函数为 $g (x) = h_{0} + h_{1} x + h_{2} x^{2} + \dots + h_{n} x^{n} + \dots$ ,计算

\begin{aligned} g (x) - 3 x g (x) = & h_{0} + (h_{1} - 3 h_{0}) x + \dots + (h_{n} - h_{n - 1}) x^{n} + \dots \\ = & 2 + (- 4) x + (- 8) x^{2} + \dots + (- 4 n) x^{n} + \dots \\ = & 2 - 4 (x + 2 x^{2} + \dots + n x^{n} + \dots) \\ = & 2 - 4 x \sum_{n = 0}^{\infty} (n + 1) x^{n} \\ = & 2 - 4 \frac{x}{(1 - x)^{2}} \end{aligned}

\begin{aligned} g (x) = & \frac{2}{1 - 3 x} - \frac{4 x}{(1 - 3 x) (1 - x)^{2}} \\ = & \frac{2}{1 - 3 x} - (\frac{A}{1 - 3 x} + \frac{B x + C}{(1 - x)^{2}}) \\ = & \frac{2}{1 - 3 x} - (\frac{3}{1 - 3 x} + \frac{x - 3}{(1 - x)^{2}}) \\ = & \frac{- 1}{1 - 3 x} + \frac{3 - x}{(1 - x)^{2}} \\ = & - \sum_{n = 0}^{\infty} (3 x)^{n} + 3 \sum_{n = 0}^{\infty} (n + 1) x^{n} - \sum_{n = 0}^{\infty} n x^{n} \\ = & \sum_{n = 0}^{\infty} (2 n + 3 - 3^{n}) x^{n} \end{aligned}

所以 $h_{n} = 2 n + 3 - 3^{n}, (n \geq 0)$ 。

EX52 👻

Solve the following two recurrence relations:
(a) $h_{n} = 2 h_{n - 1} + 5^{n}, (n \geq 1)$ with $h_{0} = 3$
(a) $h_{n} = 5 h_{n - 1} + 5^{n}, (n \geq 1)$ with $h_{0} = 3$

非齐次递推关系求解，略。

EX53

Suppose you deposit $500 in a bank account -that pays 6% interest at the end of each year (compounded annually). Thereafter, at the beginning of each year you deposit $100. Let hn be the amount in your account after n years (so h_0 = $500). Determine the generating function $g (x) = h_{0} + h_{1} x + . . . + h_{n} x^{n} + . . .$ and then a formula for $h_{n}$ .

h_{n} = 1.06 h_{n - 1} + 100, n \geq 1, h_{0} = 500

g (x) = h_{0} + h_{1} x + h_{2} x^{2} + \dots

\begin{aligned} (1 - 1.06 x) g (x) = & h_{0} + (h_{1} - 1.06 h_{0}) x + \dots + (h_{n} - h_{n - 1}) x^{n} + \dots \\ = & 500 + 100 x + 100 x^{2} + \dots + 100 x^{n} + \dots \\ = & 500 + 100 (x + x^{2} + \dots) (*) \\ = & 500 + \frac{100 x}{1 - x} \end{aligned}

\begin{aligned} g (x) = & \frac{500}{1 - 1.06 x} + \frac{100 x}{(1 - x) (1 - 1.06 x)} \\ = & \frac{500}{1 - 1.06 x} + \frac{100}{0.06} (\frac{1}{1 - 1.06 x} - \frac{1}{1 - x}) \\ = & (500 + \frac{100}{0.06}) \frac{1}{1 - 1.06 x} - \frac{100}{0.06} \frac{1}{1 - x} \\ = & (500 + \frac{100}{0.06}) \sum_{n = 0}^{\infty} (1.06 x)^{n} - \frac{100}{.0 .6} x^{n} \\ = & [(500 + \frac{100}{0.06}) (1.06)^{n} - \frac{100}{0.06}] x^{n} \end{aligned}

因此，

h_{n} = 500 (1.06)^{n} + \frac{100}{0.06} ((1.06)^{n} - 1)

提示

(*) 式不留常数凑成 $\frac{x}{1 - x}$ 的形式方便下面的分解。

EX53 另解 💡

\begin{aligned} h_{n} = & 500 (1.06)^{n} + \sum_{k = 0}^{n - 1} 100 (1.06)^{k} \\ = & 500 (1.06)^{n} + 100 \frac{(1.06)^{n} - 1}{0.06} \end{aligned}

第 7 章 递推关系和生成函数 ​

EX1 ​

EX1(a)(b) ​

EX1(c) ​

EX1(d) ​

EX2 ​

EX3 ​

EX3(b) ​

EX3PS ​

EX4 ​

EX5 ​

EX6 ⭐ ​

EX7 ⭐ ​

EX8 ​

EX9 ​

EX10 ​

EX11 ​

EX11(a) ​

EX11(b) ​

EX12 ​

EX13 ​

EX13(a) ​

EX13(b) ​

EX13(c) ​

EX13(d) ​

EX13(e) ​

EX14 ​

EX14(a) ​

EX14(b) ​

EX14(c) ​

EX14(d) ​

EX14(e) ​

EX15 ​

EX16 ​

EX17 ​

EX18 ​

EX19 ​

EX20 ​

EX21 ⭐ ​

EX22 ​

EX23 ​

EX24 ​

EX24(a) ​

EX24(b) ​

EX24(c) ​

EX24(d) ​

EX25 ​

EX26 ​

EX27 ​

EX28 ​

EX29 ​

EX30 ​

EX31 ​

EX32 ​

EX33 ​

EX34 ​

EX35 ​

EX36 ​

EX37 ​

EX38 👻 ​

EX38(b) ​

EX39 ​

EX40 ​

EX41 ​

EX42 👻 ​

EX43 👻 ​

EX44 👻 ​

EX45 👻 ​

EX46 👻 ​

EX47 👻 ​

EX48 👻 ​

EX48(b) ​

EX48(f) ​

EX49 ​

EX49PS ​

EX49 参考 ​

EX50 ​

EX51 ​

EX52 👻 ​

EX53 ​

第 7 章递推关系和生成函数

EX1

EX1(a)(b)

EX1(c)

EX1(d)

EX2

EX3

EX3(b)

EX3PS

EX4

EX5

EX6 ⭐

EX7 ⭐

EX8

EX9

EX10

EX11

EX11(a)

EX11(b)

EX12

EX13

EX13(a)

EX13(b)

EX13(c)

EX13(d)

EX13(e)

EX14

EX14(a)

EX14(b)

EX14(c)

EX14(d)

EX14(e)

EX15

EX16

EX17

EX18

EX19

EX20

EX21 ⭐

EX22

EX23

EX24

EX24(a)

EX24(b)

EX24(c)

EX24(d)

EX25

EX26

EX27

EX28

EX29

EX30

EX31

EX32

EX33

EX34

EX35

EX36

EX37

EX38 👻

EX38(b)

EX39

EX40

EX41

EX42 👻

EX43 👻

EX44 👻

EX45 👻

EX46 👻

EX47 👻

EX48 👻

EX48(b)

EX48(f)

EX49

EX49PS

EX49 参考

EX50

EX51

EX52 👻

EX53