第 6 章容斥原理及应用

错位排序的一些结论

递推公式

D_{n} = n D_{n - 1} + (- 1)^{n}, D_{n} = (n - 1) (D_{n - 2} + D_{n - 1})

常数

可以使用上面的递推公式求出来错位排序常用的一些数值， $D_{1} = 0, D_{2} = 1, D_{3} = 2, D_{4} = 9, D_{5} = 44, D_{6} = 265, D_{7} = 1854$ 。

验算代码

cpp

#include <iostream>

using namespace std;

int main()
{
    int p = 0, q = 1;
    int n;
    scanf("%d", &n);

    for(int i = 3; i <= n; ++ i) {
        int tmp = (i-1)*(p+q);
        printf("D%d = %d\n", i, tmp);
        p = q;
        q = tmp;
    }
    return 0;
}

EX1

Find the number of integers between 1 and 10,000 inclusive that are not divisible by 4,5, or 6.

本题写的详细些，后面类似的题目就不再解释太多细节。

设 $A_{i}, i = 1, 2, 3$ 分别为 1 到 10，000 之间能被 4、5 和 6 整除的个数。

计算集合大小时采用向下取整，例如 $⌊ \frac{10000}{6} ⌋ = 1666$ ，表明还取不到下一个 6 的倍数。

$A_{1} \cap A_{3}$ 表示既是 4 的倍数，也是 6 的倍数，4 和 6 的最小公倍数是 12，即能被 12 整除的数。

set	size
$A_{1}$	2500
$A_{2}$	2000
$A_{3}$	1666
$A_{1} \cap A_{2}$	500
$A_{1} \cap A_{3}$	833
$A_{2} \cap A_{3}$	333
$A_{1} \cap A_{2} \cap A_{3}$	166

\begin{aligned} | \overset{―}{A_{1}} \cap \overset{―}{A_{2}} \cap \overset{―}{A_{3}} | = & | S | - \sum | A_{i} | + \sum | A_{i} A_{j} | - \sum | A_{i} A_{j} A_{k} | \\ = & 10000 - (2500 + 2000 + 1666) + (500 + 833 + 333) - 166 \\ = & 5334 \end{aligned}

EX2

Find the number of integers between 1 and 10,000 inclusive that are not divisible by 4, 6, 7, or 10.

验证代码

cpp

#include <iostream>
#include <vector>

using namespace std;

int main()
{
    int cnt = 0;
    vector<int> arr{4, 6, 7, 10};
    for(int i = 1; i <= 10000; ++ i) {
        bool flag = true;
        for(auto item: arr) {
            if(i%item == 0) {
                flag = false;
                break;
            }
        }
        if(flag) {
            printf("%d ", i);
            cnt ++;
            if(cnt % 20 == 0) printf("\n");
        }
    }
    printf("\nTotal number = %d\n", cnt);
    return 0;
}

EX3

Find the number of integers between 1 and 10,000 that are neither perfect squares nor perfect cubes.

既是完全平方数也是完全立方数的数一定能拆分成 6 个相同数的乘积。

计算满足 $x^{2} \leq 10000, y^{3} \leq 10000, z^{6} \leq 10000$ 的最大整数解，得 $x = 100, y = 21, z = 4$ 。

set	size
$A_{1}$	100
$A_{2}$	21
$A_{1} \cap A_{2}$	4

\begin{aligned} | \overset{―}{A_{1}} \cap \overset{―}{A_{2}} | = & | S | - \sum | A_{i} | + \sum | A_{i} A_{j} | \\ = & 10000 - (100 + 21) + 4 \\ = & 9883 \end{aligned}

EX4

Determine the number of 12-combinations of the multiset
$S = {4 \cdot a, 3 \cdot b, 4 \cdot c, 5 \cdot d}$

多重集合的组合与方程的非负整数解个数等价，因此满足

0 \leq x_{1} \leq 4, 0 \leq x_{2} \leq 3, 0 \leq x_{3} \leq 4, 0 \leq x_{4} \leq 5

的方程

x_{1} + x_{2} + x_{3} + x_{4} = 12

设 $A_{i}, i = 1, 2, 3, 4$ 分别是满足 $x_{1} \geq 5, x_{2} \geq 4, x_{3} \geq 5, x_{4} \geq 6$ 的解组成的集合。

求满足 $x_{1} \geq 5$ 的解，进行变量代换 $y_{1} = x_{1} - 5, y_{2} = x_{2}, y_{3} = x_{3}, y_{4} = x_{4}$ ，方程转化为

y_{1} + y_{2} + y_{3} + y_{4} = 7

此时方程的解个数为 $(\binom{7 + 4 - 1}{7}) = 120$ ，即 $| A_{1} | = 120$ 。同理可以计算 $| A_{2} | = 165, | A_{3} | = 120, | A_{4} | = 84$ 。

求满足 $x_{1} \geq 5, x_{2} \geq 4$ 的解，进行变量代换 $y_{1} = x_{1} - 5, y_{2} = x_{2} - 4, y_{3} = x_{3}, y_{4} = x_{4}$ ，方程转化为

y_{1} + y_{2} + y_{3} + y_{4} = 3

此时方程的解个数为 $(\binom{3 + 4 - 1}{3}) = 20$ ，即 $| A_{1} \cap A_{2} | = 20$ 。

因此可以求出

set	size
$A_{1}$	120
$A_{2}$	165
$A_{3}$	120
$A_{4}$	84
$A_{1} \cap A_{2}$	20
$A_{1} \cap A_{3}$	10
$A_{1} \cap A_{4}$	4
$A_{2} \cap A_{3}$	20
$A_{2} \cap A_{4}$	10
$A_{3} \cap A_{4}$	4
$A_{1} \cap A_{2} \cap A_{3}$	0
$A_{1} \cap A_{2} \cap A_{4}$	0
$A_{1} \cap A_{3} \cap A_{4}$	0
$A_{2} \cap A_{3} \cap A_{4}$	0
$A_{1} \cap A_{2} \cap A_{3} \cap A_{4}$	0

\begin{aligned} | \overset{―}{A_{1}} \cap \overset{―}{A_{2}} \cap \overset{―}{A_{3}} \cap \overset{―}{A_{4}} | = & | S | - \sum | A_{i} | + \sum | A_{i} A_{j} | - \sum | A_{i} A_{j} A_{k} | + \sum | A_{i} A_{j} A_{k} A_{u} | \\ = & 455 - (120 + 165 + 120 + 84) + (20 + 10 + 4 + 20 + 10 + 4) \\ = & 34 \end{aligned}

EX5

Determine the number of 10-conbiations of the multiset
$S = {\infty \cdot a, 4 \cdot b, 5 \cdot c, 7 \cdot d}$

本题和上一题的区别就在于 $x_{1}$ 没有上界，不需要考虑 $x_{1}$ 上界的补集。定义 $A_{1}, A_{2}, A_{3}$ 分别表示 $x_{2} \geq 5, x_{3} \geq 6, x_{4} \geq 8$ 。

set	size
$A_{1}$	$(\binom{8}{3}) = 56$
$A_{2}$	$(\binom{7}{3}) = 35$
$A_{3}$	$(\binom{5}{3}) = 10$
$A_{1} \cap A_{2}$	0
$A_{1} \cap A_{3}$	0
$A_{2} \cap A_{3}$	0
$A_{1} \cap A_{2} \cap A_{3}$	0

\begin{aligned} | \overset{―}{A_{1}} \cap \overset{―}{A_{2}} \cap \overset{―}{A_{3}} | = & | S | - \sum | A_{i} | + \sum | A_{i} A_{j} | - \sum | A_{i} A_{j} A_{k} | \\ = & 286 - (56 + 35 + 10) \\ = & 185 \end{aligned}

EX6

A bakery sells chocolate, cinnamon, and plain doughnuts and at a particular time has 6 chocolate, 6 cinnamon, and 3 plain. If a box contains 12 doughnuts, how many different options are there for a box of oughnuts?

该问题可以转化为方程

x_{1} + x_{2} + x_{3} = 12

在 $0 \leq x_{1} \leq 6, 0 \leq x_{2} \leq 6, 0 \leq x_{3} \leq 3$ 的条件下整数解的个数。

定义 $A_{1}, A_{2}, A_{3}$ 分别表示 $x_{1} \geq 7, x_{2} \geq 7, x_{3} \geq 4$ 。

set	size
$A_{1}$	$(\binom{7}{2}) = 21$
$A_{2}$	$(\binom{7}{2}) = 21$
$A_{3}$	$(\binom{10}{2}) = 45$
$A_{1} \cap A_{2}$	0
$A_{1} \cap A_{3}$	$(\binom{3}{2})$ = 3
$A_{2} \cap A_{3}$	$(\binom{3}{2}) = 3$
$A_{1} \cap A_{2} \cap A_{3}$	0

\begin{aligned} | \overset{―}{A_{1}} \cap \overset{―}{A_{2}} \cap \overset{―}{A_{3}} | = & | S | - \sum | A_{i} | + \sum | A_{i} A_{j} | - \sum | A_{i} A_{j} A_{k} | \\ = & (\binom{12 + 2}{2}) - (21 + 21 + 45) + (3 + 3) \\ = & 91 - (21 + 21 + 45) + (3 + 3) \\ = & 10 \end{aligned}

EX7

Determine the number of solutions of the equation $x_{1} + x_{2} + x_{3} + x_{4} = 14$ in nonnegative integers $x_{1}, x_{2}, x_{3}$ , and $x_{4}$ not exceeding 8.

本题可以利用对称性减少计算，

\begin{aligned} | \overset{―}{A_{1}} \cap \overset{―}{A_{2}} \cap \overset{―}{A_{3}} \cap \overset{―}{A_{4}} | = & (\binom{17}{3}) - 4 (\binom{8}{3}) \\ = & 680 - 4 \times 56 \\ = & 456 \end{aligned}

EX8

Determine the number of solutions of the equation $x_{1} + x_{2} + x_{3} + x_{4} + x_{5} = 14$ in positive integers $x_{1}, x_{2}, x_{3}, x_{4}$ , and $x_{5}$ not exceeding 5.

类似上一题，不过本题强调正（positive）整数，取值范围因此是 $1 \leq x_{i} \leq 5$ ，先平移变成 $0 \leq y_{i} \leq 4$ ，求解方程 $\sum y_{i} = 9$ 。

\begin{aligned} | \overset{―}{A_{1}} \cap \overset{―}{A_{2}} \cap \overset{―}{A_{3}} \cap \overset{―}{A_{4}} \cap \overset{―}{A_{5}} | = & (\binom{13}{4}) - 5 (\binom{8}{4}) + (\binom{5}{2}) (\binom{3}{4}) \\ = & 715 - 5 \times 70 + 10 \times 0 \\ = & 365 \end{aligned}

EX9 👻

Determine the number of integral solutions of the equation
$x_{1} + x_{2} + x_{3} + x_{4} = 20$
that satisfy
$1 \leq x_{1} \leq 6, 0 \leq x_{2} \leq 7, 4 \leq x_{3} \leq 8, 2 \leq x_{4} \leq 6$

过程略，答案 96。

EX10

Let S be a multiset with k distinct objects with given repetition numbers $n_{l}, n_{2}, . . ., n_{k}$ , respectively. Let r be a positive integer such that there is at least one r-combination of S. Show that, in applying the inclusion-exclusion principle to determine the number of r-combinations of S, one has $A_{1} \cap A_{2} \cap . . . \cap A_{k} = \emptyset$ .

多重集合 r 组合问题转化为方程 $\sum_{i = 0}^{k} x_{i} = r, 0 \leq x_{i} \leq n_{i}$ 的整数解问题。

假设存在一组解，因此有 $r \leq \sum_{i = 0}^{k} n_{i}$ ，记 $A_{i}$ 为满足 $x_{i} > n_{i}$ 的集合。

当 $A_{1} \cap A_{2} \cap . . . \cap A_{k} \neq \emptyset$ ，即存在 $r = \sum_{i = 0}^{k} x_{i} > \sum_{i = 0}^{k} n_{i} \geq r$ ，产生矛盾，所以 $A_{1} \cap A_{2} \cap . . . \cap A_{k} = \emptyset$ 。

CAUTION

本题的奇怪之处就在于题目没告诉这些 $A_{1}$ 、 $A_{2}$ 等究竟是什么，这是参考答案中突然定义的。

EX11

Determine the number of permutations of {1, 2, ... ,8} in which no even integer is in its natural position.

\begin{aligned} | \overset{―}{A_{1}} \cap \overset{―}{A_{2}} \cap \overset{―}{A_{3}} \cap \overset{―}{A_{4}} | = & 8! - 4 \times 7! + (\binom{4}{2}) \times 6! + (\binom{4}{3}) \times 5! + 4! \\ = & 715 - 5 \times 70 + 10 \times 0 \\ = & 24024 \end{aligned}

EX12

Determine the number of permutations of {1, 2, ... ,8} in which exactly four integers are in their natural positions.

选出 4 个数放入自然位置，剩余 4 个数进行错位排序。

D_{4} = 4! (1 - \frac{1}{1!} + \frac{1}{2!} - \frac{1}{3!} + \frac{1}{4!}) = 9

因此总排列数为，

(\binom{8}{4}) \times D_{4} = 70 \times 9 = 630

提示

n 元素错位排序可以直接使用公式，

D_{n} = n! (1 - \frac{1}{1!} + \frac{1}{2!} - \frac{1}{3!} + \dots + (- 1)^{n} \frac{1}{n!})

EX13

Determine the number of permutations of {1, 2, ... ,9} in which at least one odd integer is in its natural position.

设 $A_{i}$ 表示 i 在自然位置上，

set	size
$A_{i}$	$8!$
$A_{i} \cap A_{j}$	$7!$
$A_{i} \cap A_{j} \cap A_{k}$	$6!$
$A_{i} \cap A_{j} \cap A_{k} \cap A_{u}$	$5!$
$A_{i} \cap A_{j} \cap A_{k} \cap A_{u} \cap A_{v}$	$4!$

\begin{aligned} | A_{1} \cup A_{3} \cup A_{5} \cup A_{7} \cup A_{9} | = & S - | \overset{―}{A_{1}} \cap \overset{―}{A_{3}} \cap \overset{―}{A_{5}} \cap \overset{―}{A_{7}} \cap \overset{―}{A_{9}} | \\ = & 5 \times 8! - (\binom{5}{2}) \times 7! + (\binom{5}{3}) \times 6! - 5 \times 5! + 4! \\ = & 157824 \end{aligned}

提示

本题考查定理 6.1.2（正文 p102）至少具有性质的计数。大多数题目还是考察定理 6.1.1 不具有性质的容斥原理。

EX14

Determine a general formula for the number of permutations of the set {1, 2, ... , n} in which exactly k integers are in their natural positions.

选 k 个放到自然位置，其余 n-k 个进行错位排序。

(\binom{n}{k}) D_{n - k}

EX15

At a party, seven gentlemen check their hats. In how many ways can their hats be returned so that (a) no gentleman receives his own hat? (b) at least one of the gentlemen receives his own hat? (c) at least two of the gentlemen receive their own hats?

EX15Q(a)

进行错位排序， $D_{7} = 1854$ 。

EX15Q(b)

全排序减去错位排序（没有人在自然位置），即至少有一个在自然位置。 $7! - D_{7} = 3186$ 。

EX15Q(c)

从上一问的结果（至少有一人在自然位置）中减去恰有一人在自然位置的情况，即至少有两人在自然位置， $3186 - 7 D_{6} = 3186 - 7 \times 265 = 1331$ 。

EX16

Use combinatorial reasoning to derive the identity
$n! = (\binom{n}{0}) D_{0} + (\binom{n}{1}) D_{n - 1} + (\binom{n}{2}) D_{n - 2} + \dots + (\binom{n}{n - 1}) D_{1} + (\binom{n}{n}) D_{0}$
(Here, $D_{0}$ is defined to be 1.)

记 $S$ 为 ${1, 2, \dots, n}$ 的全排列集合， $S_{i}$ 表示恰有 i 个元素在自然位置的排序，显然 ${S_{i}}$ 划分了 $S$ ，因此 $| S | = \sum_{i = 0}^{n} | S_{i} |$ 。

全排列 $| S | = n!$ ，恰有 i 个自然位置的错位排序（参考 EX14），有 $(\binom{n}{i}) D_{n - i}$ 个，因此等式成立。

NOTE

本题定义了 $D_{0} = 1$ ，而本身的错位排序 $D_{1} = 0$ 。

EX17

Determine the number of permutations of the multiset
$S = {3 \cdot a, 4 \cdot b, 2 \cdot c}$
where, for each type of letter, the letters of the same type do not appear consecutively. (Thus abbbbcaca is not allowed, but abbbacacb is.)

设 $A_{i}, i = 1, 2, 3$ 分别表示出现了aaa、bbbb和cc， $A_{1}$ 可以当作 $a a a, b, b, b, b, c, c$ 的排列，即 $(\binom{7}{1 4 2}) = 105$ 。

set	size
$A_{1}$	105
$A_{2}$	$(\binom{6}{3 1 2}) = 60$
$A_{3}$	$(\binom{8}{3 4 1}) = 280$
$A_{1} \cap A_{2}$	$(\binom{4}{1 1 2}) = 12$
$A_{1} \cap A_{3}$	$(\binom{6}{1 4 1}) = 30$
$A_{2} \cap A_{3}$	$(\binom{5}{3 1 1}) = 20$
$A_{1} \cap A_{2} \cap A_{3}$	$(\binom{3}{1 1 1}) = 3! = 6$

\begin{aligned} | \overset{―}{A_{1}} \cap \overset{―}{A_{2}} \cap \overset{―}{A_{3}} | = & | S | - \sum | A_{i} | + \sum | A_{i} A_{j} | - \sum | A_{i} A_{j} A_{k} | \\ = & 1260 - (105 + 60 + 280) + (12 + 30 + 20) - 6 \\ = & 871 \end{aligned}

提示

本题是求的多重集合排序问题和上面的多重集合组合问题进行区分。

EX18

Verify the factorial formula
$n! = (n - 1) ((n - 2)! + (n - 1)!), (n = 2, 3, 4, . . .) .$

没太看懂这题想干什么，难道是数学归纳法？

EX19

Using the evaluation of the derangement numbers as given in Theorem 6.3.1, provide a proof of the relation
$D_{n} = (n - 1) (D_{n - 2} + D_{n - 1}), (n = 3, 4, 5, . . .) .$

展开合并同类项即可，

D_{n - 2} = (n - 2)! \sum_{i = 0}^{n - 2} \frac{(- 1)^{i}}{i!}

将 $D_{n - 1}$ 拆分为能与 $D_{n - 2}$ 同类相加的两项，

\begin{aligned} D_{n - 1} = & (n - 1)! \sum_{i = 0}^{n - 1} \frac{(- 1)^{i}}{i!} \\ = & (n - 1) \cdot (n - 2)! (\sum_{i = 0}^{n - 2} \frac{(- 1)^{i}}{i!} + \frac{(- 1)^{n - 1}}{(n - 1)!}) \\ = & (n - 1) \cdot (n - 2)! \sum_{i = 0}^{n - 2} \frac{(- 1)^{i}}{i!} + (- 1)^{n - 1} \end{aligned}

将 $D_{n - 1}$ 与 $D_{n - 2}$ 求和，

D_{n - 1} + D_{n - 2} = n \cdot (n - 2)! \sum_{i = 0}^{n - 2} \frac{(- 1)^{i}}{i!} + (- 1)^{n - 1}

(n - 1) (D_{n - 1} + D_{n - 2}) = n! \sum_{i = 0}^{n - 2} \frac{(- 1)^{i}}{i!} + (- 1)^{n - 1} (n - 1)

将 $D_{n}$ 拆分为上述形式，

\begin{aligned} D_{n} = & n! \sum_{i = 0}^{n} \frac{(- 1)^{i}}{i!} \\ = & n! \sum_{i = 0}^{n - 2} \frac{(- 1)^{i}}{i!} + n! (\frac{(- 1)^{n - 1}}{(n - 1)!} + \frac{(- 1)^{n}}{n!}) \\ = & n! \sum_{i = 0}^{n - 2} \frac{(- 1)^{i}}{i!} + (- 1)^{n - 1} n + (- 1)^{n} \\ = & (n - 1) (D_{n - 1} + D_{n - 2}) \end{aligned}

综上，等式成立。

EX20

Starting from the formula Dn = nDn- 1 + (_l)n, (n = 2,3,4, ... ), give a proof of Theorem 6.3.1.

使用数学归纳法证明，当 $n \geq 1$ 时，总有

D_{n} = n! \sum_{i = 0}^{n} \frac{(- 1)^{i}}{i!}

当 n=1 时，1 只能放在自然位置，没有错位排序，所以错位排序数为 0，且 $D_{1} = 1! \times (1 - 1) = 0$ 成立。

当 $n \geq 2$ 时，假设等式成立，对于 n+1 有

\begin{aligned} D_{n + 1} = & (n + 1) D_{n} + (- 1)^{n + 1} \\ = & (n + 1) \times n! \sum_{i = 0}^{n} \frac{(- 1)^{i}}{i!} + (- 1)^{n + 1} \\ = & (n + 1)! \sum_{i = 0}^{n} \frac{(- 1)^{i}}{i!} + (n + 1)! \times \frac{(- 1)^{n + 1}}{(n + 1)!} \\ = & (n + 1)! \sum_{i = 0}^{n + 1} \frac{(- 1)^{i}}{i!} \end{aligned}

符合等式，综上证毕。

EX21

Prove that $D_{n}$ is an even number if and only if n is an odd number.

语句 p：n 为奇数；语句 q： $D_{n}$ 为偶数。原题目可以转化为证明如下两个命题：若 p 成立，则 q 也成立；若 q 成立，则 p 也成立。

我们先考虑命题二，对于命题二我们验证它的「逆否命题」，若 $\neg q$ 成立，则 $\neg p$ 也成立。命题转化为，n 为偶数时， $D_{n}$ 为奇数。

观察式子 $D_{n} = n D_{n - 1} + (- 1)^{n}$ ，当 n 为偶数时， $n D_{n - 1}$ 项为偶数， $(- 1)^{n} = 1$ ，显然 $D_{n}$ 为奇数，命题二的逆否命题为真，命题二也为真。

对于命题一，我们采用数学归纳法证明。当 n 为奇数时，并且当 n=1 时，有 $D_{1} = 0$ ，显然成立；

当 n=2k+1( $\geq 1$ ) 时，设 $D_{2 k + 1}$ 为偶数；那么当 $n = 2 k + 3$ 时， $D_{2 k + 3} = (2 k + 3) D_{2 k + 2} + (- 1)^{(2 k + 3)} = (2 k + 3) D_{2 k + 2} - 1$ ，由命题二的逆否命题可知 $D_{2 k + 2}$ 一定为奇数，进而两个奇数的乘积 $(2 k + 3) D_{2 k + 2}$ 也为奇数，减一后为偶数。

综上，当 n 为奇数时，命题得证。

因为命题一和命题二均为真，因此可以说， $D_{n}$ 是偶数当且仅当 n 是奇数。

简评

颇有点压轴题的感觉，证明若 n 为奇数，则 $D_{n}$ 为偶数这个命题前，需要先证明若 n 为偶数，则 $D_{n}$ 为奇数。如果有前一问的引导，难度会小一些；若是直接跳跃性地构造最后一问，难度就大很多。

EX22

Show that the numbers $Q_{n}$ of Section 6.5 can be rewritten in the form
$Q_{n} = (n - 1)! (n - \frac{n - 1}{1!} + \frac{n - 2}{2} - \frac{n - 3}{3!} + \dots + \frac{(- 1)^{n - 1}}{(n - 1)!})$

对 $Q_{n}$ 定义的变形，

\begin{aligned} Q_{n} = & n! - (\binom{n - 1}{1}) (n - 1)! + (\binom{n - 1}{2}) (n - 2)! + \dots + (- 1)^{n - 1} (\binom{n - 1}{n - 1}) 1! \\ = & \sum_{k = 0}^{n - 1} (\binom{n - 1}{k}) (- 1)^{k} (n - k)! \\ = & \sum_{k = 0}^{n - 1} \frac{(n - 1)!}{k! \cdot (n - k - 1)!} \cdot (- 1)^{k} \cdot (n - k)! \\ = & (n - 1)! \sum_{k = 0}^{n - 1} (- 1)^{k} \frac{n - k}{k!} \\ = & (n - 1)! (\frac{n - 0}{0!} - \frac{n - 1}{1!} + \frac{n - 2}{2!} + \dots + (- 1)^{n - 1} \frac{n - (n - 1)}{(n - 1)!}) \\ = & (n - 1)! (n - \frac{n - 1}{1!} + \frac{n - 2}{2} - \frac{n - 3}{3!} + \dots + \frac{(- 1)^{n - 1}}{(n - 1)!}) \end{aligned}

综上，证毕。

EX23

(Continuation of Exercise 22.) Use the identity
$(- 1)^{k} \frac{n - k}{k!} = (- 1)^{k} \frac{n}{k!} + (- 1)^{k - 1} \frac{1}{(k - 1)!}$
to prove that $Q_{n} = D_{n} + D_{n - 1}, (n = 2, 3, . . .)$ .

\begin{aligned} Q_{n} = & (n - 1)! \sum_{k = 0}^{n - 1} (- 1)^{k} \frac{n - k}{k!} \\ = & (n - 1)! \sum_{k = 0}^{n - 1} ((- 1)^{k} \frac{n}{k!} + (- 1)^{k - 1} \frac{1}{(k - 1)!}) \\ = & n D_{n - 1} + (n - 1)! \sum_{k = 1}^{n - 1} \frac{(- 1)^{k - 1}}{(k - 1)!} \\ = & n D_{n - 1} + (n - 1)! \sum_{i = 0}^{n - 2} \frac{(- 1)^{i}}{(i)!} \\ = & n D_{n - 1} + (n - 1) D_{n - 2} \\ = & D_{n - 1} + (n - 1) (D_{n - 1} + D_{n - 2}), for D_{n} = (n - 1) (D_{n - 1} + D_{n - 2}) \\ = & D_{n} + D_{n - 1} \end{aligned}

提示

该解法需要使用 $D_{n} = (n - 1) (D_{n - 1} + D_{n - 2})$ 的化简技巧，答案的则是巧妙地添加了一个为 0 的项 $(- 1)^{n} \frac{n - n}{n!}$ ，进而，

Q_{n} = (n - 1)! \sum_{k = 0}^{n} (- 1)^{k} \frac{n - k}{k!}

在之后的展开项中则分别是 $D_{n}, D_{n - 1}$ 的定义形式。

EX24

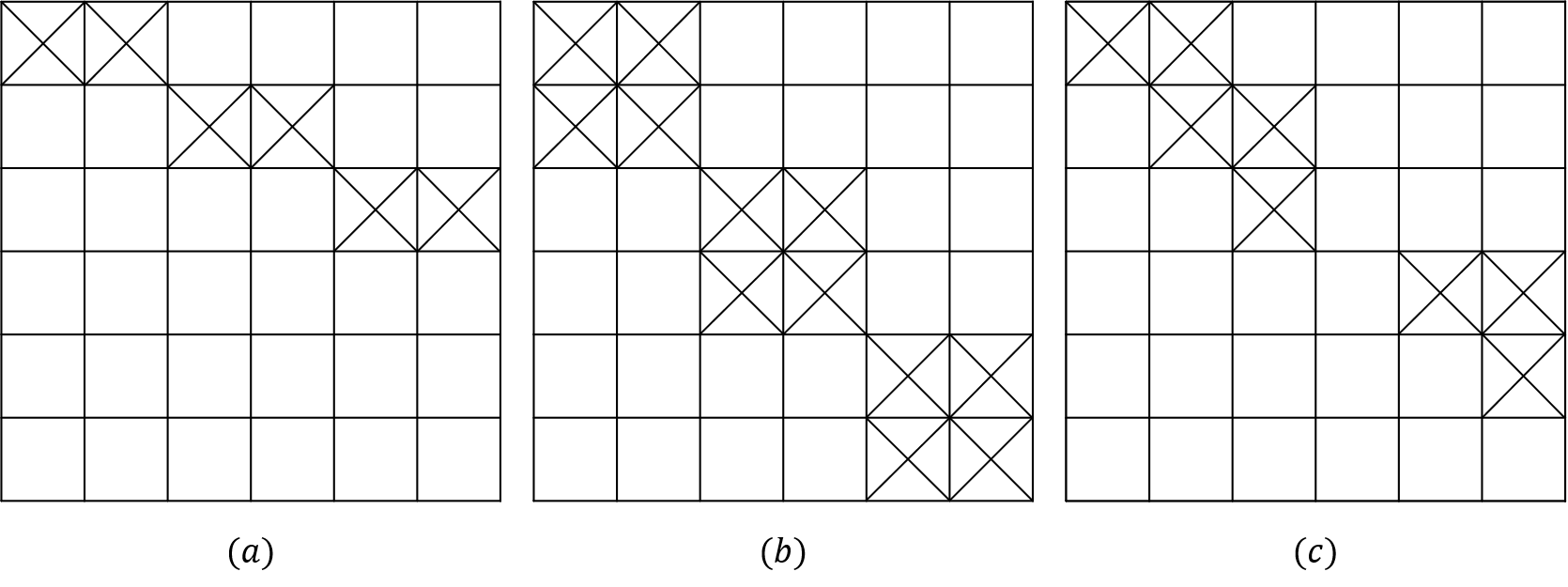
What is the number of ways to place six nonattacking rooks on the 6-by-6 boards with forbidden positions as shown?

设 $r_{k}$ 为在 k 个禁止位上摆放棋子的方法数，

EX24 Q(a)

显然， $r_{0} = 1, r_{1} = 6$ ，禁止位置的集合可以划分为 3 个独立的部分，每一部分最多只能放置一辆车。

因此， $r_{2} = (\binom{3}{2}) \times 2^{2} = 12, r_{3} = (\binom{3}{3}) 2^{3} = 8$ 。

禁止位置上无法摆放四辆及以上的车，因此， $r_{i} = 0, i \geq 4$ 。

综上，可以列表，

$k$	0	1	2	3	4	5	6
$r_{k}$	1	6	12	8	0	0	0

并且计算摆放的方法数。

\sum_{k = 0}^{n} r_{k} (- 1)^{k} (n - k)! = 1 \times 6! - 6 \times 5! + 12 \times 4! - 8 \times 3! = 240

EX24 Q(b)

r_{2} = 3 \times 2 + (\binom{3}{2}) \times 4^{2} = 54

r_{3} = (\binom{3}{1}) \times 2 \times (\binom{2}{1}) \times 4 + 4^{3} = 112

r_{4} = (\binom{3}{2}) \times 2^{2} + (\binom{3}{1}) \times 2 \times 4^{2} = 108

r_{5} = (\binom{3}{2}) \times 2^{2} \times 4 = 48

r_{6} = 2^{3} = 8

$k$	0	1	2	3	4	5	6
$r_{k}$	1	12	54	112	108	48	8

\sum_{k = 0}^{n} r_{k} (- 1)^{k} (n - k)! = 1 \times 6! - 12 \times 5! + 54 \times 4! - 112 \times 3! + 108 \times 2! - 48 \times 1! + 8 \times 0! = 80

EX24 Q(c)

将棋盘禁止位分为相互独立的 $F_{1}$ 和 $F_{2}$ ，分别求出 $F_{1}$ 和 $F_{2}$ 能摆放车的方法数，如下表

$k$	0	1	2	3
$F_{1} (k)$	1	5	6	1

$k$	0	1	2
$F_{2} (k)$	1	3	1

进而求出 $r_{k} = \sum_{j = 0}^{k} F_{1} (j) F_{2} (k - j)$ ，

$k$	0	1	2	3	4	5	6
$r_{k}$	1	8	22	24	9	1	0

\sum_{k = 0}^{n} r_{k} (- 1)^{k} (n - k)! = 1 \times 6! - 8 \times 5! + 22 \times 4! - 24 \times 3! + 9 \times 2! - 1 \times 1! + 0 \times 0! = 161

EX25

Count the permutations $i_{1} i_{2} i_{3} i_{4} i_{5} i_{6}$ of {1, 2, 3, 4, 5, 6}, where $i_{1} \neq 1, 5, i_{3} \neq 2, 3, 5; i_{4} \neq 4;$ and $i_{6} \neq 5, 6$ .

该问题等价于棋盘问题，可以把不等式转化为每一行（列）限制的序号，本题画出图像后可以发现，有 4 个大小为 1 的禁止块，2 个大小为 2 的禁止块。

从行的角度来思考，最多放置 4 个车，因为只有 4 行有禁止位，所以 $r_{5} = r_{6} = 0$ 。

对于 $r_{2}$ 的计算方法是：先固定一个，寻找另一个可能的位置，因此 $r_{2} = 6 + 4 + 3 + 3 + 2 + 2 = 20$ 。

r_{3} = (3 + 3 + 2 + 2) + (2 + 2 + 1) + (2) + (2) + (1) = 20 r + 4 = 2 + 2 + 2 + 1 = 7

$k$	0	1	2	3	4	5	6
$r_{k}$	1	8	20	20	7	0	0

\sum_{k = 0}^{n} r_{k} (- 1)^{k} (n - k)! = 1 \times 6! - 8 \times 5! + 20 \times 4! - 20 \times 3! + 7 \times 2! - 0 \times 1! + 0 \times 0! = 134

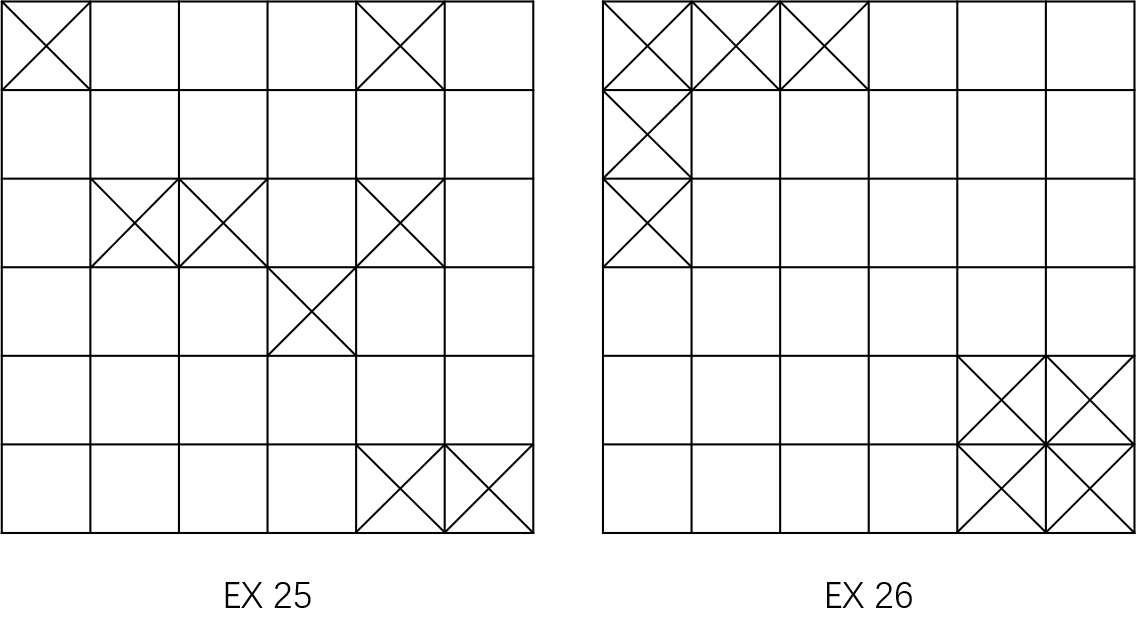
EX25 & EX26

EX25PS

本题与其他禁止位放车问题的区别是：本题不太容易拆分成几个独立的部分。

EX26

Count the permutations $i_{1} i_{2} i_{3} i_{4} i_{5} i_{6}$ of {1, 2, 3, 4,5, 6}, where $i_{1} \neq 1, 2, 3; i_{2} \neq 1; i_{3} \neq 1; i_{5} \neq 5, 6$ and $i_{6} \neq 5, 6$ .

题目转化过程同 EX25，不过这次计算类似 EX24。将棋盘禁止位置划分为 $F_{1}, F_{2}$ 。

对于每一部分，先计算摆放车可能的种类数，

$k$	0	1	2	3
$F_{1} (k)$	1	5	4	0

$k$	0	1	2	3
$F_{2} (k)$	1	4	2	0

r_{k} = \sum_{i = 0}^{n} F_{1} (i) \times F_{2} (k - i)

$k$	0	1	2	3	4	5	6
$r_{k}$	1	9	26	26	8	0	0

\sum_{k = 0}^{n} r_{k} (- 1)^{k} (n - k)! = 1 \times 6! - 9 \times 5! + 26 \times 4! - 26 \times 3! + 8 \times 2! = 124

EX27

A carousel has eight seats, each representing a different animal. Eight girls are seated on the carousel facing forward (each girl ooks at another girl's back). In how many ways can the girls change seats so that each has a different girl in front of her? How does the problem change if all the seats are identical?

设 8 个位置的座位编号分别为 $1, 2, . . ., 8$ ，并且 i 号座位面向 i+1 号座位（ $1 \leq i \leq 7$ ），8 号座位面向 1 号座位。

第 i 个女孩分别坐在 i 号座位上，重排后坐到 $s_{i}$ 号座位上，并且要求 $s_{i}$ 不能面向 $s_{i + 1}$ ，（ $s_{8}$ 不能面向 $s_{1}$ ）。

记 $A_{i}$ 表示排列 $s_{1} s_{2} \dots s_{8}$ 中 $s_{i}$ 面向 $s_{i + 1}$ （其中 $1 \leq i \leq 7$ ）， $A_{8}$ 表示表示排列 $s_{1} s_{2} \dots s_{8}$ 中 $s_{8}$ 面向 $s_{1}$ 。

对于 $| A_{1} |$ ，有 8 种方式决定 $s_{1}$ ， $s_{2}$ 只能在前面，有 1 种方式，其余可以随意排列。因此 $| A_{1} | = 8 \times 1 \times 6!$ 。 $| A_{i} |$ 同理。

对于 $| A_{1} \cap A_{2} |$ ，有 8 种方式决定 $s_{1} s_{2} s_{3}$ ；其余可以随意排列。因此 $| A_{1} \cap A_{2} | = 8 \times 5!$ ，其余 $| A_{i} \cap A_{j} |$ 同理。

\begin{aligned} | \overset{―}{A_{1}} \cap \overset{―}{A_{2}} \cap \dots \cap \overset{―}{A_{4}} | = & | S | - \sum | A_{i} | + \sum | A_{i} A_{j} | - \dots + \sum | A_{1} A_{2} \dots A_{7} A_{8} | \\ = & 8! - (\binom{8}{1}) \times 8 \times 6! + (\binom{8}{2}) \times 8 \times 5! - \dots + 8 \\ = & 13000 \end{aligned}

当所有座位都相同时，第一个选择座位的女孩只有 1 种选法，破环后，其余人选法不变，因此排列总数为 $13000 / 8 = 1625$ 。

EX27PS

参考答案给的符号有些歧义， $A_{i}$ 和 $A_{s}$ 表示的含义不一样，但符号相同，如 $| A_{1} |$ 对前者（ $| A_{i = 1} |$ ）来说，是 $s_{1}$ 面向 $s_{2}$ 的情况；对于后者（ $| A_{s = 1} |$ ）来说则是所有 1 个交集的情况 $\sum | A_{i} |$ 。

EX28

A carousel has eight seats, each representing a different animal. Eight boys are seated on the carousel but facing inward, so that each boy faces another (each boy looks at another boy's front). In how many ways can the boys change seats so that each faces a different boy? How does the problem change if all the seats are dentical?

第 i 个男孩坐在 i 号座位上，重排后坐到 $s_{i}$ 号座位上。设 $A_{i}$ 表示 $s_{i}$ 与 $s_{i + 4}$ 面对面（ $1 \leq i \leq 4$ ），因此需要求所有 i 与 i+4 没有面对面的情况，即 $| \overset{―}{A_{1}} \cap \overset{―}{A_{2}} \cap \overset{―}{A_{3}} \cap \overset{―}{A_{4}} |$ 。

对于 $| A_{1} |$ ，有 8 种方式决定 $s_{1}$ ， $s_{5}$ 只能在对面，有 1 种方式，其余可以随意排列。因此 $| A_{1} | = 8 \times 1 \times 6!$ 。 $| A_{2} | ， | A_{3} |, | A_{4} |$ 同理。

对于 $| A_{1} \cap A_{2} |$ ，有 8 种方式决定 $s_{1}$ ， $s_{5}$ 随之确定；有 6 种方式确定 $s_{2}$ ， $s_{6}$ 也随之确定，其余可以随意排列。因此 $| A_{1} \cap A_{2} | = 8 \times 6 \times 4!$ ，其余 $| A_{i} \cap A_{j} |$ 同理。

\begin{aligned} | \overset{―}{A_{1}} \cap \overset{―}{A_{2}} \cap \overset{―}{A_{3}} \cap \overset{―}{A_{4}} | = & | S | - \sum | A_{i} | + \sum | A_{i} A_{j} | - \sum | A_{i} A_{j} A_{k} | + \sum | A_{i} A_{j} A_{k} A_{u} | \\ = & 8! - (\binom{4}{1}) (8 \times 6!) + (\binom{4}{2}) (8 \times 6 \times 4!) - (\binom{4}{3}) (8 \times 6 \times 4 \times 2!) + (\binom{4}{4}) (8 \times 6 \times 4 \times 2) \\ = & 23040 \end{aligned}

当所有座位都相同时，则变成了换排列，因此排列总数为 $23040 / 8 = 2880$ 。

EX29

A subway has six stops on its route from its base location. There are 10 people on the subway as it departs its base location. Each person exits the subway at one of its six stops, and at each stop at least one person exits. In how many ways can this happen?

如果没有任何限制，10 个人一共有 $6^{10}$ 种下车方案。设 $A_{i}$ 表示没人在 i 车站下车，所以有 $| A_{i} | = 5^{10}$ ；对于 $| A_{i} \cap A_{j} | = 4^{10}$ 。同理，可以计算多个子集车站没人下车的情况。

\begin{aligned} | \overset{―}{A_{1}} \cap \overset{―}{A_{2}} \cap \dots \cap \overset{―}{A_{6}} | = & | S | - \sum | A_{i} | + \sum | A_{i} A_{j} | - \dots + \sum | A_{1} A_{2} \dots A_{6} | \\ = & 6^{10} + (- 1)^{k} (\binom{6}{k}) (6 - k)^{1} 0 \\ = & 6^{10} - 6 \times 5^{10} + 15 \times 4^{10} - 20 \times 3^{10} + 15 \times 2^{10} - 6 \times 1^{10} + 1 \times 0^{10} \\ = & 1165626 \end{aligned}

EX30

How many circular permutations are there of the multiset
${3 \cdot a, 4 \cdot b, 2 \cdot c, 1 \cdot d},$
where, for each type of letter, all letters of that type do not appear consecutively?

设 $A_{i}, i = 1, 2, 3$ 分别表示出现了aaa、bbbb和cc， $A_{1}$ 可以当作 $a a a, b, b, b, b, c, c, d$ 的循环排列，即 $\frac{1}{8} \times (\binom{8}{1 4 2}) = 105$ 。

set	size
$A_{1}$	105
$A_{2}$	60
$A_{3}$	280
$A_{1} \cap A_{2}$	12
$A_{1} \cap A_{3}$	30
$A_{2} \cap A_{3}$	20
$A_{1} \cap A_{2} \cap A_{3}$	3

\begin{aligned} | \overset{―}{A_{1}} \cap \overset{―}{A_{2}} \cap \overset{―}{A_{3}} | = & | S | - \sum | A_{i} | + \sum | A_{i} A_{j} | - \sum | A_{i} A_{j} A_{k} | \\ = & \frac{1}{10} \times \frac{10!}{3! \cdot 4! \cdot 2! \cdot 1!} - (105 + 60 + 280) + (12 + 30 + 20) - 3 \\ = & 1260 - (105 + 60 + 280) + (12 + 30 + 20) - 3 \\ = & 874 \end{aligned}

顺便一提

参考答案认为一个 d 本身就是所有的 d 连续出现。

Since d appears in the multiset with multiplicity one, it is vacuously true that for any circular permutation of the multiset, all occurrences of d will appear consecutively.

当然，最后解题时还是认为连续最起码要有一前一后的两项才算连续，所谓连续，参考 EX17，甚至本题数据和结果都与这题一致。

EX31

How many circular permutations are there of the multiset
${2 \cdot a, 3 \cdot b, 4 \cdot c, 5 \cdot d},$
where, for each type of letter, all letters of that type do not appear consecutively?

设 $A_{i}, i = 1, 2, 3, 4$ 分别表示出现了aa、bbb、ccccc和ddddd， $A_{1}$ 可以当作 $a a, b, b, b, c, c, c, c, d, d, d, d, d$ 的循环排列，即 $\frac{1}{13} \times (\binom{13}{1 3 4 5}) = 27720$ 。

set	size
$A_{1}$	27720
$A_{2}$	6930
$A_{3}$	2520
$A_{4}$	1260
$A_{1} \cap A_{2}$	1260
$A_{1} \cap A_{3}$	504
$A_{1} \cap A_{4}$	280
$A_{2} \cap A_{3}$	168
$A_{2} \cap A_{4}$	105
$A_{3} \cap A_{4}$	60
$A_{1} \cap A_{2} \cap A_{3}$	42
$A_{1} \cap A_{2} \cap A_{4}$	30
$A_{1} \cap A_{3} \cap A_{4}$	20
$ A_2 \cap A_3 \cap A_4$	12
$A_{1} \cap A_{2} \cap A_{3} \cap A_{4}$	6

\begin{aligned} | \overset{―}{A_{1}} \cap \overset{―}{A_{2}} \cap \overset{―}{A_{3}} \cap \overset{―}{A_{4}} | = & | S | - \sum | A_{i} | + \sum | A_{i} A_{j} | - \sum | A_{i} A_{j} A_{k} | + \sum | A_{i} A_{j} A_{k} A_{u} | \\ = & \frac{1}{14} \times \frac{14!}{2! \cdot 3! \cdot 4! \cdot 5!} - \\ (27720 + 6930 + 2520 + 1260) + \\ (1260 + 504 + 280 + 168 + 105 + 60) - \\ (42 + 30 + 20 + 12) + 6 \\ = & 180180 - (27720 + 6930 + 2520 + 1260) + \\ (1260 + 504 + 280 + 168 + 105 + 60) - (42 + 30 + 20 + 12) + 6 \\ = & 144029 \end{aligned}

EX32-40 说明 🚧 👻

后面的题目似乎都是 6.5 小结莫比乌斯反演的练习题。

其中 EX32 是关键的 🔑 题目； EX33 是加星题目（*）； EX36 是带有禁止位置的放车问题，虽然指明了用 6.5 中的解题方法。但用 EX24 中的方法也能很快做出答案（6 种）。

第 6 章 容斥原理及应用 ​

错位排序的一些结论 ​

递推公式 ​

常数 ​

EX1 ​

EX2 ​

EX3 ​

EX4 ​

EX5 ​

EX6 ​

EX7 ​

EX8 ​

EX9 👻 ​

EX10 ​

EX11 ​

EX12 ​

EX13 ​

EX14 ​

EX15 ​

EX15Q(a) ​

EX15Q(b) ​

EX15Q(c) ​

EX16 ​

EX17 ​

EX18 ​

EX19 ​

EX20 ​

EX21 ​

EX22 ​

EX23 ​

EX24 ​

EX24 Q(a) ​

EX24 Q(b) ​

EX24 Q(c) ​

EX25 ​

EX25PS ​

EX26 ​

EX27 ​

EX27PS ​

EX28 ​

EX29 ​

EX30 ​

EX31 ​

EX32-40 说明 🚧 👻 ​